题目内容
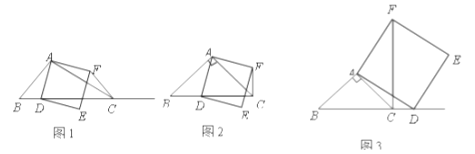
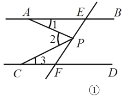
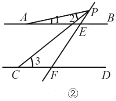
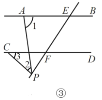
【题目】如图所示，点B、F、C、E在同一直线上，AC、DF相交于G，AB⊥BE，垂足为B，DE⊥BE，垂足为E，且AB=DE,BF＝CE.
求证：（1）△ABC≌△DEF；
（2）如果∠ACB=25°,求∠AGF的度数？
【答案】（1）见解析；（2）50°
【解析】
（1）根据SAS即可证得结论；（2）利用全等三角形的性质和三角形的外角性质定理即可求出结果.
（1）∵AB⊥BE，DE⊥BE，
∴∠ABC=∠DEF=90，
∵BF＝CE，
∴BF+CF=CE+CF，即BC=EF.
在Rt△ACB和Rt△DEF中，
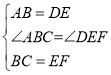
∴△ABC≌△DEF(SAS)；
（2）∵△ABC≌△DEF，
∴∠ACB=∠DFE，
∵∠ACB=25°，
∴∠DFE=25°，
∴∠AGF=∠DFE+∠ACB=50°.
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
【题目】某公司生产的一种健身产品在市场上受到普遍欢迎，每年可在国内、国外市场上全部售完．该公司的年产量为6000件，若在国内市场销售，平均每件产品的利润与国内销售量
的关系如下表：
销售量 |
|
|
单件利润（元） |
|
|
若在国外销售，平均每件产品的利润与国外的销售数量
的关系如下表：
销售量 |
|
|
单件利润（元） | 100 |
|
（1）用的代数式表示为：=；
（2）该公司每年国内、国外的销售量各为多少时，可使公司每年的总利润为60万元？
