题目内容
【题目】已知直线![]() 平行
平行![]() ,直线
,直线![]() 分别截
分别截![]() 、
、![]() 于点
于点![]() 、
、![]() 两点.
两点.
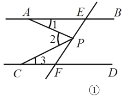
(1)如图①,有一动点![]() 在线段
在线段![]() 之间运动(不与E,F两点重合),试探究
之间运动(不与E,F两点重合),试探究![]() 、
、![]() 、
、![]() 的等量等关系?试说明理由.
的等量等关系?试说明理由.
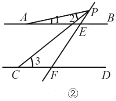
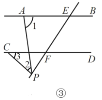
(2)如图②、③,当动点![]() 在线段
在线段![]() 之外运动(不与E,F两点重合),问上述结论是否还成立?若不成立,试写出新的结论并说明理由.
之外运动(不与E,F两点重合),问上述结论是否还成立?若不成立,试写出新的结论并说明理由.
【答案】(1)∠2=∠1+∠3,理由见解析;(2)∠2=∠1+∠3不成立,新的结论为∠2=![]() ,理由见解析.
,理由见解析.
【解析】
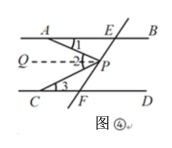
(1)如图④,过点 P作PQ∥AB,则∠1=∠APQ,根据平行线的性质,即可得到结论;
(2)分两种情况:(i)当点P在FE的延长线上时,如图⑤,过点 P作PQ∥AB,(ii)当点P在EF的延长线上时,如图⑥,过点 P作PQ∥AB,分别求出∠2、∠1、∠3的数量关系,即可得到结论.
(1)∠2=∠1+∠3,理由如下:
如图④,过点 P作PQ∥AB,则∠1=∠APQ.
∵AB∥CD,PQ∥AB,
∴PQ∥CD,
∴∠3=∠CPQ.
∵∠2=∠APQ+∠CPQ=∠1+∠3;
(2)∠2=∠1+∠3 不成立,新的结论为∠2=![]() .理由如下:
.理由如下:
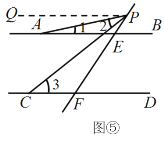
(i)当点P在FE的延长线上时,
如图⑤,过点 P作PQ∥AB,则∠1=∠APQ.
∵AB∥CD,PQ∥AB,
∴PQ∥CD,
∴∠3=∠CPQ.
∴∠2=∠CPQ![]() ∠APQ=∠3
∠APQ=∠3![]() ∠1;
∠1;
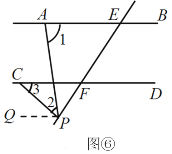
(ii)当点P在EF的延长线上时,
如图⑥,过点 P作PQ∥AB,则∠1=∠APQ.
∵AB∥CD,PQ∥AB,
∴PQ∥CD,
∴∠3=∠CPQ,
∴∠2=∠APQ![]() ∠CPQ=∠1
∠CPQ=∠1![]() ∠3.
∠3.
综上所述:∠2=![]() .
.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目