题目内容
如图①②③…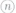 ,M,N分别是⊙O的内接正三角形A1A2A3,方形A1A2A3A4,正五边形A1A2A3A4A5,…,正n边形A1A2A3…An的边A1A2,A2A3上的点,且A2M=A3N,连接OM,ON.
,M,N分别是⊙O的内接正三角形A1A2A3,方形A1A2A3A4,正五边形A1A2A3A4A5,…,正n边形A1A2A3…An的边A1A2,A2A3上的点,且A2M=A3N,连接OM,ON.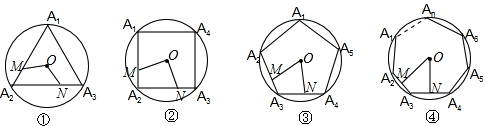
(1)求图①中∠MON的度教.
(2)图②中∠MON的度数是
(3)试探究∠MON的度数与正n边形边数n的关系.(直接写出答案)
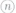 ,M,N分别是⊙O的内接正三角形A1A2A3,方形A1A2A3A4,正五边形A1A2A3A4A5,…,正n边形A1A2A3…An的边A1A2,A2A3上的点,且A2M=A3N,连接OM,ON.
,M,N分别是⊙O的内接正三角形A1A2A3,方形A1A2A3A4,正五边形A1A2A3A4A5,…,正n边形A1A2A3…An的边A1A2,A2A3上的点,且A2M=A3N,连接OM,ON.
(1)求图①中∠MON的度教.
(2)图②中∠MON的度数是
90°
90°
,图③∠MON的度数是72°
72°
.(3)试探究∠MON的度数与正n边形边数n的关系.(直接写出答案)
分析:(1)连接OA2、OA3,先利用SAS证明△OMA2≌△ONA3,得出∠A2OM=∠A3ON,则∠MON=∠A2OA3,再由正n边形的中心角为
即可求出∠A2OA3=120°;
(2)同(1)即可解答;
(3)由(1)、(2)找出规律,即可解答.
| 360° |
| n |
(2)同(1)即可解答;
(3)由(1)、(2)找出规律,即可解答.
解答:解: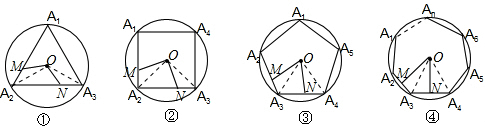 (1)如图①,连接OA2、OA3,
(1)如图①,连接OA2、OA3,
∵A1A2=A1A3,
∴∠A1A2A3=∠A1A3A2,
∵OA3=OA2,O是外接圆的圆心,
∴A3O平分∠A1A3A2,
∴∠OA2A3=∠OA3A2=30°,
∴∠OA2M=∠OA3N=30°,
∵A2M=A3N,OA2=OA3,
∴△OMA2≌△ONA3,
∴∠A2OM=∠A3ON,
∴∠MON=∠A2OA3,
∵∠A2OA3=
=120°;
∴∠MON=∠A2OA3=120°;
(2)如图②,连接OA2、OA3,
易证△OMA2≌△ONA3,
∴∠A2OM=∠A3ON,
∴∠MON=∠A2OA3,
∵∠A2OA3=
=90°;
∴∠MON=∠A2OA3=90°;
如图③,连接OA3、OA4,
易证△OMA3≌△ONA4,
∴∠A3OM=∠A4ON,
∴∠MON=∠A3OA4,
∵∠A3OA4=
=72°;
∴∠MON=∠A3OA4=72°;
(3)由图①可知,n=3时,∠MON=
=120°;
在图②中,n=4时,∠MON=
=90°;
在图③中,n=5时,∠MON=
=72°;
…,
则正多边形的边数为n时,∠MON=
.
故答案为90°,72°.
 (1)如图①,连接OA2、OA3,
(1)如图①,连接OA2、OA3,∵A1A2=A1A3,
∴∠A1A2A3=∠A1A3A2,
∵OA3=OA2,O是外接圆的圆心,
∴A3O平分∠A1A3A2,
∴∠OA2A3=∠OA3A2=30°,
∴∠OA2M=∠OA3N=30°,
∵A2M=A3N,OA2=OA3,
∴△OMA2≌△ONA3,
∴∠A2OM=∠A3ON,
∴∠MON=∠A2OA3,
∵∠A2OA3=
| 360° |
| 3 |
∴∠MON=∠A2OA3=120°;
(2)如图②,连接OA2、OA3,
易证△OMA2≌△ONA3,
∴∠A2OM=∠A3ON,
∴∠MON=∠A2OA3,
∵∠A2OA3=
| 360° |
| 4 |
∴∠MON=∠A2OA3=90°;
如图③,连接OA3、OA4,
易证△OMA3≌△ONA4,
∴∠A3OM=∠A4ON,
∴∠MON=∠A3OA4,
∵∠A3OA4=
| 360° |
| 5 |
∴∠MON=∠A3OA4=72°;
(3)由图①可知,n=3时,∠MON=
| 360° |
| 3 |
在图②中,n=4时,∠MON=
| 360° |
| 4 |
在图③中,n=5时,∠MON=
| 360° |
| 5 |
…,
则正多边形的边数为n时,∠MON=
| 360° |
| n |
故答案为90°,72°.
点评:本题考查的是正多边形和圆,根据题意作出辅助线,构造出全等三角形是解答此题的关键,注意正多边形外接圆的圆心与其中心重合.

练习册系列答案
相关题目
 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB= 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.