题目内容
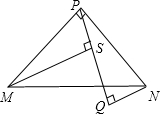 如图,在△MPN中,MP=NP,∠MPN=90°,NQ⊥PQ,MS⊥PQ,垂足分别为Q、S.
如图,在△MPN中,MP=NP,∠MPN=90°,NQ⊥PQ,MS⊥PQ,垂足分别为Q、S.(1)试说明:△PMS≌△NPQ;
(2)若QS=3.5cm,NQ=2.1cm,求MS的长.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)求出∠PSM=∠Q=∠MPN=90°,∠PMS=∠NPQ,根据AAS证出全等即可;
(2)根据全等得出MS=PQ,PS=NQ=2.1cm,代入MS=PQ=QS+PS求出即可.
(2)根据全等得出MS=PQ,PS=NQ=2.1cm,代入MS=PQ=QS+PS求出即可.
解答:(1)解:∵∠MPN=90°,NQ⊥PQ,MS⊥PQ,
∴∠PSM=∠Q=∠MPN=90°,
∴∠SPM+∠PMS=90°,∠SPM+∠NPQ=90°,
∴∠PMS=∠NPQ,
在△PMS和△NPQ中
∴△PMS≌△NPQ(AAS);
(2)解:∵QS=3.5cm,NQ=2.1cm,△PMS≌△NPQ,
∴MS=PQ,PS=NQ=2.1cm,
∴MS=PQ=QS+PS=2.1cm+3.5cm=5.6cm.
∴∠PSM=∠Q=∠MPN=90°,
∴∠SPM+∠PMS=90°,∠SPM+∠NPQ=90°,
∴∠PMS=∠NPQ,
在△PMS和△NPQ中
|
∴△PMS≌△NPQ(AAS);
(2)解:∵QS=3.5cm,NQ=2.1cm,△PMS≌△NPQ,
∴MS=PQ,PS=NQ=2.1cm,
∴MS=PQ=QS+PS=2.1cm+3.5cm=5.6cm.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,SSS,AAS,全等三角形的对应边相等.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
在同一平面上,已知线段AB的长为10厘米,点A、B到直线L的距离分别为6厘米和4厘米,则符合条件的直线L的条数为( )
| A、2 条 | B、3条 |
| C、4条 | D、无数条 |
下列调查中,适合用全面调查方式的是( )
| A、了解我市60岁以上老人的健康情况 |
| B、了解我校八(3)班学生课外阅读的情况 |
| C、了解一批炮弹的杀伤半径 |
| D、了解一批袋装食品是否含有防腐剂 |
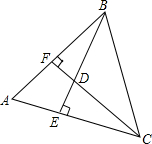 如图,已知AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D,由这些条件写出所有相等的线段,并说明理由.
如图,已知AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D,由这些条件写出所有相等的线段,并说明理由. 如图,在△ABC中,AB=8,BC=6,S△ABC=12.试求tan∠B的值.
如图,在△ABC中,AB=8,BC=6,S△ABC=12.试求tan∠B的值.