题目内容
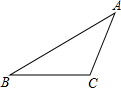如图，在△ABC中，AB=8，BC=6，S△ABC=12．试求tan∠B的值．考点：锐角三角函数的定义,勾股定理
专题：计算题
分析：过点A作AD⊥BC的延长线于D，利用三角形的面积求出AD，再利用勾股定理列式求出BD，然后根据锐角的正切值等于对边比邻边列式计算即可得解．
解答：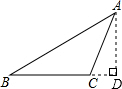
解：如图，过点A作AD⊥BC的延长线于D，
S△ABC=
BC•AD=
×6•AD=12，
解得AD=4，
在Rt△ABD中，BD=
=
=4
，
tan∠B=
=
=
．
解：如图，过点A作AD⊥BC的延长线于D，S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
解得AD=4，
在Rt△ABD中，BD=
| AB2-AD2 |
| 82-42 |
| 3 |
tan∠B=
| AD |
| BD |
| 4 | ||
4
|
| ||
| 3 |
点评：本题考查了锐角三角函数的定义，勾股定理，作出辅助线构造成直角三角形是解题的关键．
练习册系列答案
相关题目
已知关于x的一元二次方程x2-px+q=0有两个根，则这两个根是（ ）
A、x=
| ||||
B、x=
| ||||
C、x=
| ||||
D、x=
|
在以下各对数中，是方程组
的解的是（ ）
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
如图，有甲、乙两张对边平行的纸条，将这两张纸条交叉重叠地放在一起，重合部分为四边形NMGH．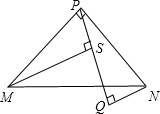
如图，在△MPN中，MP=NP，∠MPN=90°，NQ⊥PQ，MS⊥PQ，垂足分别为Q、S．
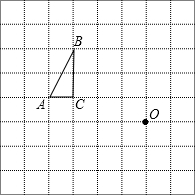如图，每个小方格都是边长为1个单位长度的小正方形．