题目内容
观察下列等式:
第一行 22-12=4-1=3
第二行 32-22=9-4=5
第三行 42-32=16-9=7
第四行 52-42=25-16=9
…
(1)请你写出第五行的等式为________.
(2)按照上述规律,第n行的等式为________.
(3)请你利用已学过的知识对你得到的等式进行证明.
解:(1)把原等式变形得:
第一行 (1+1)2-12=4-1=3=2×1+1;
第二行 (2+1)2-22=9-4=5=2×2+1;
第三行 (3+1)2-32=16-9=7=2×3+1;
第四行 (4+1)2-42=25-16=9=2×4+1;
则第五行的等式为(5+1)2-52=36-25=11=2×5+1,即62-52=36-25=11,
(2)按照上述规律,第n行的等式为:(n+1)2-n2=2n+1,
(3)证明:等式左边=[(n+1)+n][(n+1)-n]=2n+1=右边,得证.
故答案为:(1)62-52=36-25=11;(2)(n+1)2-n2=2n+1
分析:(1)观察原题中的等式发现,被减数的底数比行数多1,且减数的底数等于行数,而计算结果是从3开始的奇数,从而得到第5行的等式;
(2)根据上述规律,同理猜想得到第n行的等式;
(3)利用平方差公式化简(2)的等式左边,合并后得到与等式的右边相等,得证.
点评:此题考查了平方差公式的灵活运用,考查了学生提出猜想,证明猜想,归纳总结得出结论的能力,是一道规律型的基础题.
第一行 (1+1)2-12=4-1=3=2×1+1;
第二行 (2+1)2-22=9-4=5=2×2+1;
第三行 (3+1)2-32=16-9=7=2×3+1;
第四行 (4+1)2-42=25-16=9=2×4+1;
则第五行的等式为(5+1)2-52=36-25=11=2×5+1,即62-52=36-25=11,
(2)按照上述规律,第n行的等式为:(n+1)2-n2=2n+1,
(3)证明:等式左边=[(n+1)+n][(n+1)-n]=2n+1=右边,得证.
故答案为:(1)62-52=36-25=11;(2)(n+1)2-n2=2n+1
分析:(1)观察原题中的等式发现,被减数的底数比行数多1,且减数的底数等于行数,而计算结果是从3开始的奇数,从而得到第5行的等式;
(2)根据上述规律,同理猜想得到第n行的等式;
(3)利用平方差公式化简(2)的等式左边,合并后得到与等式的右边相等,得证.
点评:此题考查了平方差公式的灵活运用,考查了学生提出猜想,证明猜想,归纳总结得出结论的能力,是一道规律型的基础题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
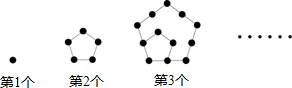 (1)用棋子按下列方式摆图形,依照此规律,第n个图形有
(1)用棋子按下列方式摆图形,依照此规律,第n个图形有