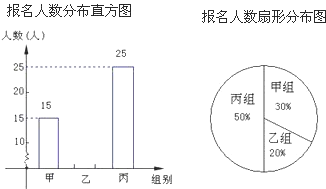
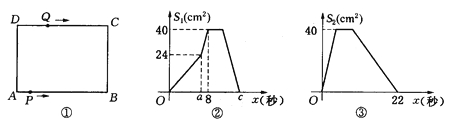
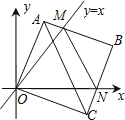
��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����Ϊ��4��1���������߽�y���ڵ�A����x����B��C���㣨��B�ڵ�C����ࣩ����֪C������Ϊ��6��0����

��1����������ߵĽ���ʽ��
��2����֪��P���������ϵ�һ�����㣬��λ��A��C����֮�䣮�ʣ�����P�˶���ʲôλ��ʱ����PAC�������������PAC����������
��3������AB������B��AB�Ĵ��߽��������ڵ�D���Ե�CΪԲ�ĵ�Բ�������ߵĶԳ���l���У��Ȳ�ȫͼ�Σ����ж�ֱ��BD����C��λ�ù�ϵ������֤����
���𰸡���1��y=��![]() x2+2x��3����2��P���λ���ǣ�3��
x2+2x��3����2��P���λ���ǣ�3��![]() ������PAC����������
������PAC����������![]() ����3��P���λ���ǣ�3��
����3��P���λ���ǣ�3��![]() ������PAC����������
������PAC����������![]() ��
��
��������
�����������1���������߶���Ϊ��4��1����������䶥��ʽy=a��x��4��2+1����C�㣨6��0���������м������a��ֵ��
��2�����P�����꣨m����![]() m2+2m��3�����ú�m�Ķ���ʽ����ʾ����PAC��������ݽ⼫ֵ���⼴�ɵó���PAC�����ȡ���ֵʱP������꣬�Լ�������ֵ��
m2+2m��3�����ú�m�Ķ���ʽ����ʾ����PAC��������ݽ⼫ֵ���⼴�ɵó���PAC�����ȡ���ֵʱP������꣬�Լ�������ֵ��
��3����ͼ���ø����ߣ����������������εı�����ϵ���C��ֱ��BD�ľ��룬������C�뾶���бȽϣ����ɵó����ۣ�
��1���⣺�������ߵĶ���Ϊ��4��1����
���������߽���ʽΪy=a��x��4��2+1��
�������߾�����C��6��0����
��0=a��6��4��2+1�����a=��![]() ��
��
��y=��![]() ��x��4��2+1=��
��x��4��2+1=��![]() x2+2x��3��
x2+2x��3��
���������ߵĽ���ʽΪy=��![]() x2+2x��3��
x2+2x��3��
��2���⣺��ͼ1������P��ƽ����y���ֱ�߽�AC�ڵ�Q��
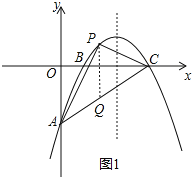
��A��0����3����C��6��0����
��ֱ��AC����ʽΪy=![]() x��3��
x��3��
��P��������m����![]() m2+2m��3����
m2+2m��3����
��Q���������m��![]() m��3����
m��3����
��PQ=��![]() m2+2m��3����
m2+2m��3����![]() m��3��=��
m��3��=��![]() m2+
m2+![]() m��
m��
��S��PAC=S��PAQ+S��PCQ=![]() ������
������![]() m2+
m2+![]() m����6=��
m����6=��![]() ��m��3��2+
��m��3��2+![]() ��
��
����m=3ʱ����PAC��������Ϊ![]() ��
��
����m=3ʱ����![]() m2+2m��3=
m2+2m��3=![]() ��
��
��P��������3��![]() ����
����
���ϣ�P���λ���ǣ�3��![]() ������PAC����������
������PAC����������![]() ��
��
��3���ж�ֱ��BD����C���룮
֤�����![]() ��x��4��2+1=0�����x1=2��x2=6��
��x��4��2+1=0�����x1=2��x2=6��
��B�����꣨2��0����
���������߽�y���ڵ�A��
��A��������0����3����
��AB=![]() =
=![]() ��
��
����C��Գ���l�����ڵ�F������C�İ뾶CF=2��
��CE��BD�ڵ�E����ͼ2������BEC=��AOB=90����
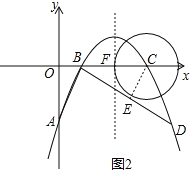
�ߡ�ABD=90����
���CBE=90������ABO��
���ߡ�BAO=90������ABO��
���BAO=��CBE��
���AOB�ס�BEC��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��CE=![]() ��2��
��2��
��ֱ��BD����C���룮