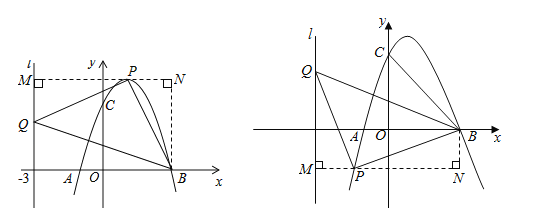��Ŀ����
����Ŀ����ͼ��������L��![]() ��x�ύ��A��B��3��0�����㣨A��B����ࣩ����y�ύ�ڵ�C��0��3������֪�Գ���x=1��
��x�ύ��A��B��3��0�����㣨A��B����ࣩ����y�ύ�ڵ�C��0��3������֪�Գ���x=1��
��1����������L�Ľ���ʽ��
��2����������L����ƽ��h����λ���ȣ�ʹƽ�ƺ����������ߵĶ���������OBC�ڣ�������OBC�ı߽磩����h��ȡֵ��Χ��
��3�����P��������L����һ�㣬��Q��ֱ��l��x=��3�ϣ���PBQ�ܷ��Ϊ�Ե�PΪֱ�Ƕ���ĵ���ֱ�������Σ����ܣ�������������ĵ�P�����ꣻ�����ܣ���˵�����ɣ�

���𰸡���1��![]() ����2��2��h��4����3��P��1��4������0��3������
����2��2��h��4����3��P��1��4������0��3������![]() ��
��![]() ������
������![]() ��
��![]() ����
����
��������
�����������1�����ô���ϵ������������ߵĽ���ʽ���ɣ�
��2�������ֱ��BC����ʽΪy=��x+3������������߶������꣬�ó���x=1ʱ��y=2����������߶��������ɵó������
��3����P��m��![]() ����Q����3��n������3����P��m��
����Q����3��n������3����P��m��![]() ����Q����3��n����������������ۣ��ٵ�P����x���Ϸ�ʱ����P����PM��ֱ��y�ᣬ��y����M�㣬��B����BN��ֱ��MP���ӳ�����N�㣬��֤����PQM�ա�BPN��AAS�����õ�PM=BN����PM=BN=
����Q����3��n����������������ۣ��ٵ�P����x���Ϸ�ʱ����P����PM��ֱ��y�ᣬ��y����M�㣬��B����BN��ֱ��MP���ӳ�����N�㣬��֤����PQM�ա�BPN��AAS�����õ�PM=BN����PM=BN=![]() ������B������ɵ�PN=3��m����PM+PN=6���õ�
������B������ɵ�PN=3��m����PM+PN=6���õ�![]() �������̼�����
�������̼�����
�ڵ�P����x���·�ʱ����P����PM��ֱ��l��M�㣬��B����BN��ֱ��MP���ӳ�����N�㣬ͬ���ɵ���PQM�ա�BPN���õ�PM=BN�� PM=6����3��m��=3+m��BN=![]() ����
����![]() ���ⷽ�̼�����
���ⷽ�̼�����
�����������1���������ߵĶԳ���x=1��B��3��0������A����1��0����
��������![]() ����C��0��3��������x=0ʱ��c=3��
����C��0��3��������x=0ʱ��c=3��
����������![]() ����A����1��0����B��3��0������
����A����1��0����B��3��0������![]() ����
����![]() ���������ߵĽ���ʽΪ��
���������ߵĽ���ʽΪ��![]() ��
��
��2����C��0��3����B��3��0������ֱ��BC����ʽΪy=��x+3����![]() =
=![]() ��������������1��4��
��������������1��4��
������ֱ��BC��y=��x+1����x=1ʱ��y=2����������L����ƽ��h����λ���ȣ�����h=2ʱ�������߶�������BC�ϣ�
��h=4ʱ�������߶�������OB�ϣ�����������L����ƽ��h����λ���ȣ�ʹƽ�ƺ����������ߵĶ���������OBC�ڣ�������OBC�ı߽磩����2��h��4��
��3����P��m��![]() ����Q����3��n����������������ۣ�
����Q����3��n����������������ۣ�
�ٵ�P����x���Ϸ�ʱ����P����PM��ֱ��y�ᣬ��y����M�㣬��B����BN��ֱ��MP���ӳ�����N�㣬��ͼ��ʾ����B��3��0�����ߡ�PBQ���Ե�PΪֱ�Ƕ���ĵ���ֱ�������Σ����BPQ=90�㣬BP=PQ������PMQ=��BNP=90�㣬��MPQ=��NBP������PQM����BPN�У��ߡ�PMQ=��BNP����MPQ=��BNP��PQ=BP�����PQM�ա�BPN��AAS������PM=BN����PM=BN=![]() ������B������ɵ�PN=3��m����PM+PN=6����
������B������ɵ�PN=3��m����PM+PN=6����![]() ����ã�m=1��m=0����P��1��4����P��0��3����
����ã�m=1��m=0����P��1��4����P��0��3����
�ڵ�P����x���·�ʱ����P����PM��ֱ��l��M�㣬��B����BN��ֱ��MP���ӳ�����N�㣬ͬ���ɵ���PQM�ա�BPN����PM=BN����PM=6����3��m��=3+m��BN=![]() ����
����![]() �����m=
�����m=![]() ��
��![]() ����P��
����P��![]() ��
��![]() ����
����![]() ��
��![]() ����
����
���Ͽɵã����������ĵ�P�������ǣ�1��4������0��3������![]() ��
��![]() ���ͣ�
���ͣ�![]() ��
��![]() ����
����