题目内容
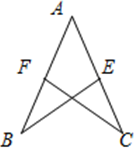
如图,已知AC平分∠PAQ,点B、B′分别在边AP、AQ上,如果添加一个条件,即可推出AB=A B′,那么该条件不可以是( )
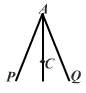
A.BB′⊥AC B.CB=CB′ C.∠ACB=∠ACB′ D.∠ABC=∠AB′C

A.BB′⊥AC B.CB=CB′ C.∠ACB=∠ACB′ D.∠ABC=∠AB′C
B.
试题分析:如图:∵AC平分∠PAQ,点B,B′分别在边AP,AQ上,
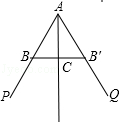
A:若BB′⊥AC,在△ABC与△AB′C中,∠BAC=∠B′AC,AC=AC,∠ACB=∠ACB′,∴△ABC≌△AB′C,∴AB=AB′;
B:若BC=B′C,不能证明△ABC≌△AB′C,即不能证明AB=AB′;
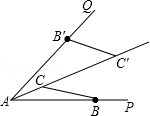
C:若∠ACB=∠ACB′,则在△ABC与△AB'C中,∠BAC=∠B′AC,AC=AC,∴△ABC≌△AB′C,∴AB=AB′;
D:若∠ABC=∠AB′C,则∠ACB=∠ACB′∠BAC=∠B′AC,AC=AC,∴△ABC≌△AB′C,∴AB=AB′.
故选B.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
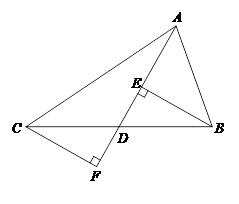
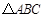 与
与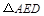 均是等边三角形,连接BE、CD.请在图中找出一条与
均是等边三角形,连接BE、CD.请在图中找出一条与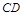 长度相等的线段,并证明你的结论.
长度相等的线段,并证明你的结论.