题目内容
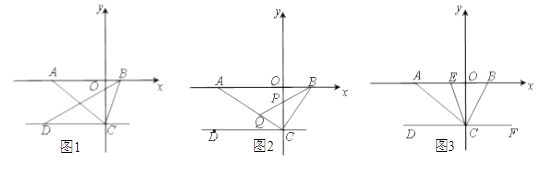
【题目】如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.易证:CE=CF.
(1)在图1中,若G在AD上,且∠GCE=450.试猜想GE,BE,GD三线段之间的数量关系,并证明你的结论.
(2)运用(1)中解答所积累的经验和知识,完成下面两题:
①如图2,在四边形ABCD中∠B=∠D=900,BC=CD,点E,点G分别是AB边,AD边上的动点.若∠BCD=α,∠ECG=β,试探索当α和β满足什么关系时,图1中GE,BE,GD三线段之间的关系仍然成立,并说明理由.
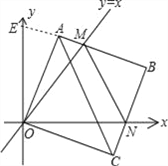
②在平面直角坐标中,边长为1的正方形OABC的两顶点A,C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图3).设△MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化?若不变,请直接写出结论.
【答案】(1)GE=BE+GD,证明见解析;(2)①α=2β,理由见解析;<span style="color: rgb(169, 68, 66); font-family: Meiryo; font-size: 15.3333px; line-height: 23px; background-color: rgb(245, 245, 245);">②</span>在旋转正方形OABC的过程中,p值无变化.理由见解析.
【解析】试题分析:(1)易知△CBE≌△CDF,易证得∠ECF=∠BCD=90°,又由∠GCE=45°,可得∠GCF=∠GCE=45°,即可证得△ECG≌△FCG,继而可得GE=BE+GD;(2) ①α=2β,延长AD到F点,使DF=BE,连接CF,可证△EBC≌△FDC,即GE=BE+GD;②在旋转正方形OABC的过程中,p值无变化.延长BA交y轴于E点,可以得出△OAE≌△OCN,△OME≌△OMN,p=MN+BN+BM=AM+CN+BN+BM=AB+BC=2.
试题解析:
(1)∵在△EBC和△FDC中,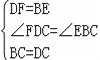 ∴△EBC≌△FDC,∴∠DCF=∠BCE,
∴△EBC≌△FDC,∴∠DCF=∠BCE,
∵∠GCE=45°,∴∠BCE+∠DCG=90°﹣45°=45°,即∠DCG+∠DCF=45°,∴GC=GC,ECG=∠FCG,
在△ECG和△FCG中,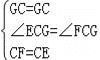 ,∴△ECG≌△FCG,∴EG=GF,即GE=BE+GD.
,∴△ECG≌△FCG,∴EG=GF,即GE=BE+GD.
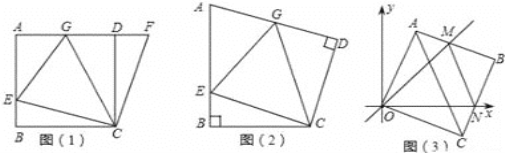
(2)①α=2β.如图,
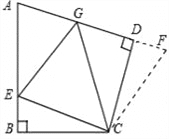
延长AD到F点,使DF=BE,连接CF,可证△EBC≌△FDC,
则∠BCE+∠DCG=∠GCF,由α=2β可知∠ECG=∠GCF,可证△ECG≌△FCG,故EG=GF,即GE=BE+GD.
②在旋转正方形OABC的过程中,p值无变化.
证明:如图,
延长BA交y轴于E点,则∠AOE=45°﹣∠AOM,∠CON=90°﹣45°﹣∠AOM=45°﹣∠AOM,
∴∠AOE=∠CON.又∵OA=OC,∠OAE=180°﹣90°=90°=∠OCN.
在△OAE和△OCN中,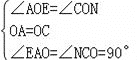 .∴△OAE≌△OCN(ASA).∴OE=ON,AE=CN.
.∴△OAE≌△OCN(ASA).∴OE=ON,AE=CN.
在△OME和△OMN中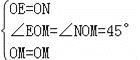 .∴△OME≌△OMN(SAS).∴MN=ME=AM+AE.
.∴△OME≌△OMN(SAS).∴MN=ME=AM+AE.
∴MN=AM+CN,∴p=MN+BN+BM=AM+CN+BN+BM=AB+BC=2.
∴在旋转正方形OABC的过程中,p值无变化.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案