题目内容
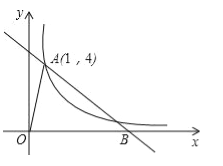
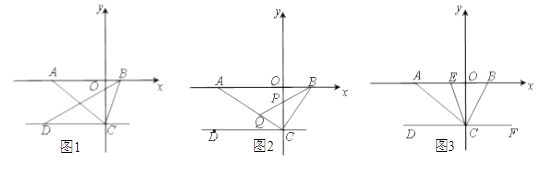
【题目】如图1,在平面直角坐标系中,点![]() 为
为![]() 轴负半轴上一点,点
轴负半轴上一点,点![]() 为
为![]() 轴正半轴上一点,
轴正半轴上一点,![]() ,
,![]() ,其中
,其中![]() ,
,![]() 满足关系式:
满足关系式:![]() +
+![]() .
.
(1)![]() = ,
= ,![]() = ,△
= ,△![]() 的面积为 ;
的面积为 ;
(2)如图2,若![]() ⊥
⊥![]() ,点
,点![]() 线段
线段![]() 上一点,连接
上一点,连接![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,当∠
,当∠![]() =∠
=∠![]() 时,求证:
时,求证:![]() 平分∠
平分∠![]() ;
;
(3)如图3,若![]() ⊥
⊥![]() ,点
,点![]() 是点
是点![]() 与点
与点![]() 之间一动点,连接
之间一动点,连接![]() ,
,![]() 始终平分∠
始终平分∠![]() ,当点
,当点![]() 在点
在点![]() 与点
与点![]() 之间运动时,
之间运动时,![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.
【答案】(1)![]() =-3,
=-3,![]() = -4,△
= -4,△![]() 的面积为6; (2)证明见解析;
的面积为6; (2)证明见解析;
(3) ![]() 的值是定值,
的值是定值,![]() =2,理由见解析.
=2,理由见解析.
【解析】试题分析:(1)由非负数的性质即可求出a、b的值,由题意可得DC的长以及DC边上的高,根据三角形的面积公式即可求得;
(2)由AC⊥BC可得∠CBQ+∠CQP=90°,又∠OBP+∠OPB=90°,∠OPB=∠CPQ,∠CPQ=∠CQP从而可得∠CBQ=∠OBP,从而问题得证;
(3)由AC⊥BC,可得∠ACB=90°,从而可得∠ACD+∠BCF=90°,由CB平分∠ECF可得∠ACD+∠ECB=90°,而已知∠ACE+∠ECB=90°,从而可得∠ACD=∠ACE,得∠DCE=2∠ACD,
从而能够得到∠ACD=∠BCO, 由已知可得CD//AB,从而得到结论.
试题解析:(1)![]() = -3,
= -3,![]() =-4,△
=-4,△![]() 的面积为6;
的面积为6;
(2)∵AC⊥BC,∴∠CBQ+∠CQP=90°,又∵∠OBP+∠OPB=90°,∠OPB=∠CPQ,
∴∠CPQ+∠OBP=90°,又∵∠CPQ=∠CQP,∴∠CBQ=∠OBP,∴BP平分∠ABC ;
(3) ![]() 的值是定值,
的值是定值,![]() =2,理由如下:
=2,理由如下:
∵AC⊥BC,∴∠ACB=90°,∴∠ACD+∠BCF=90°,
又∵CB平分∠ECF,∴∠ECB=∠BCF,∴∠ACD+∠ECB=90°,
又∵∠ACE+∠ECB=90°,∴∠ACD=∠ACE,∴∠DCE=2∠ACD,
又∵∠ACD+∠ACO=90°,∠BCO+∠ACO=90°,∴∠ACD=∠BCO,
又∵C(0,-3),D(-4,-3), ∴CD//AB,∴∠BEC=∠DCE=2∠ACD,∴∠BEC=2∠BCO,
∴![]() =2.
=2.