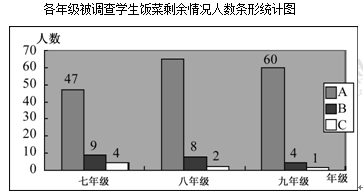
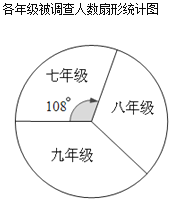
题目内容
【题目】如图,已知△ABC中,∠B=90°,AB=BC,BD=CE,M是AC边上的中点。
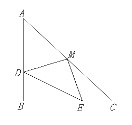
(1)求证:△DEM是等腰直角三角形.
(2)已知AD=4,CE=3,求DE的长。
【答案】(1)详见解析;(2)5.
【解析】
试题分析:(1)连接BM,根据等腰直角三角形的性质可得BM⊥AC,∠DBM=45°,BM=CM=![]() AC,然后利用“边角边”证明△BDM和△CEM全等,根据全等三角形对应边相等可得DM=EM,全等三角形对应角相等可得∠BMD=∠CME,再求出∠DME=90°,从而判定为△DEM是等腰直角三角形.(2)由(1)得BD=CE=3,再根据AB=BC可得AD=BE=4,在Rt△DBE中,根据勾股定理即可求得DE的长.
AC,然后利用“边角边”证明△BDM和△CEM全等,根据全等三角形对应边相等可得DM=EM,全等三角形对应角相等可得∠BMD=∠CME,再求出∠DME=90°,从而判定为△DEM是等腰直角三角形.(2)由(1)得BD=CE=3,再根据AB=BC可得AD=BE=4,在Rt△DBE中,根据勾股定理即可求得DE的长.
试题解析:解:(1)连接BM,
∵AB=AC,∠B=90°,M是AC的中点,
∴BM⊥AC,∠DBM=45°,BM=CM=![]() AC,
AC,
在△BDM和△CEM中,
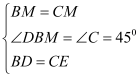 ,
,
∴△BDM≌△CEM(SAS),
∴DM=EM,∠BMD=∠CME,
∴∠DME=∠BMD+∠BME=∠CME+∠BME=∠BMC=90°,
∴△DEM是等腰直角三角形.
由(1)得BD=CE=3,
∵AB=BC
∴AD=BE=4,
在Rt△DBE中,根据勾股定理可得DE=5.

【题目】甲,乙两班举行电脑汉字输入速度比赛,参赛学生每分钟输入汉字的个数经统计计算后,结果如下。 某同学根据上表分析,得出如下结论。
班级 | 参加人数 | 中位数 | 方差 | 平均数 |
甲 | 55 | 149 | 191 | 135 |
乙 | 55 | 151 | 110 | 135 |
(1)甲,乙两班学生成绩的平均水平相同。
(2)乙班优秀的人数多于甲班优秀的人数。(每分钟输入汉字≧150个为优秀。)
(3)甲班成绩的波动情况比乙班成绩的波动小。
上述结论中正确的是( )
A.(1) (2) (3)B.(1) (2)C.(1) (3)D.(2)(3)
【题目】如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
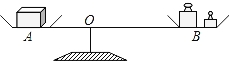
x(cm) | 10 | 15 | 20 | 25 | 30 |
y(g) | 30 | 20 | 15 | 12 | 10 |
(1)猜测y与x之间的函数关系,求出函数关系式并加以验证;
(2)当砝码的质量为24g时,活动托盘B与点O的距离是多少?
(3)将活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?