Question

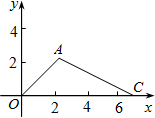在平面直角坐标中，已知A、C两点的坐标分别为A（

5

，

5

）、C（3

5

，0）．
（1）求△OAC的面积．
（2）在第一、二象限内是否存在点B，使以O、A、B、C为顶点的四边形为平行四边形？若存在，请求出所有符合条件的点B的坐标；若不存在，请说明理由．

Answer 1

分析：（1）根据C点横坐标求OC，根据A点纵坐标求OC边上的高，可求△OAC的面积；
（2）存在，利用平移的方法，将A点向左（或向右）平移OC的长度，可得符合条件的点B的坐标．

解答：解：（1）由C（3

5

，0）可知，OC=3

5

，
由A（

5

，

5

）可知，△OAC的OC边上高为

5

，
所以，S_△OAC=

1

2

×3

5

×

5

=7.5；
（2）存在．
将A点向左（或向右）平移3

5

，得符合条件的点B，
此时，B点坐标为（

5

-3

5

，

5

）或（

5

+3

5

，

5

），
即B（-2

5

，

5

）或（4

5

，

5

），

点评：本题考查了一次函数的综合运用．关键是根据点的坐标求三角形的底和高，利用平移的方法，求平行四边形的第四个顶点坐标．