题目内容
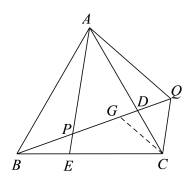
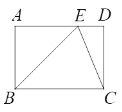
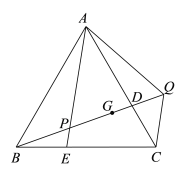
【题目】如图,在等边△ABC中,点D是AC上的一点,在BC上取一点E,使BE=CD,连接AE交BD于点P,在BD的延长线上取一点Q,使AP=PQ,连接AQ、CQ,点G为PQ的中点,DG=PE,若CQ=![]() ,则BQ=________________.
,则BQ=________________.
【答案】![]()
【解析】
如下图,连接CG,由已知条件易证△ABE≌△BCD,由此可得∠BAE=∠CBD,从而可得∠APQ=∠BAE+∠ABP=∠ABC=60°,结合AP=PQ可得△APQ是等边三角形,由此易证△ABP≌△ACQ,从而可得BP=CQ=![]() ,再通过证∠BEP=∠CDG,证得△BEP≌△CDG可得CG=BP=CQ,∠CGD=∠BPE=∠APD=60°,由此可得△CGQ是等边三角形,由此可得GQ=CQ=
,再通过证∠BEP=∠CDG,证得△BEP≌△CDG可得CG=BP=CQ,∠CGD=∠BPE=∠APD=60°,由此可得△CGQ是等边三角形,由此可得GQ=CQ=![]() ,结合点G是PQ的中点可得PQ=
,结合点G是PQ的中点可得PQ=![]() ,由此即可得到BQ=
,由此即可得到BQ=![]() .
.
如下图,连接CQ,∵△ABC是等边三角形,
∴AB=BC,∠ABE=∠BCD=60°,
∵BE=CD,
∴△ABE≌△BCD,
∴∠BAE=∠CBD,
∴∠APQ=∠BAE+∠ABD=∠CBD+∠ABD=∠ABC=60°,
∵AP=PQ,
∴△APQ是等边三角形,
∴∠PAQ=∠BAC=60°,AP=AQ,
∴∠BAC-∠EAC=∠PAQ-∠EAC,即∠BAP=∠CAQ,
∴△BAP≌△CAQ,
∴BP=CQ=![]() ,
,
∵∠BEP=∠ACB+∠CAE=60°+∠CAE,∠CDG=∠APQ+∠CAE=60°+∠CAE,
∴∠BEP=∠CDG,
又∵BE=CD,PE=DG,
∴△BEP≌△CDG,
∴CG=BP=CQ,∠PBE=∠GCD,
∴∠DGC=∠PBE+∠GCB=∠GCD+∠GCB=∠DCB=60°,
∴△GCD是等边三角形,
∴GQ=CQ=![]() ,
,
又∵点G是PQ的中点,
∴PQ=2GQ=![]() ,
,
∴BQ=BP+PQ=![]() .
.
故答案为:![]() .
.