题目内容
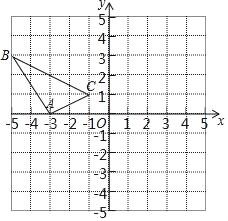
【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到△A2B2C2;
(2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
【答案】(1)画图见解析;(2)(0,2).
【解析】
(1)根据中心对称和平移性质分别作出变换后三顶点的对应点,再顺次连接可得;
(2)根据中心对称的概念即可判断.
(1)如图所示,△A1B1C1和△A2B2C2即为所求;
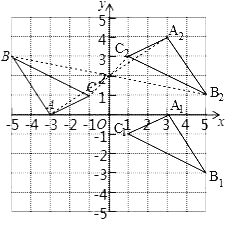
(2)由图可知,△A2B2C2与△ABC关于点(0,2)成中心对称.
点睛:本题考查了中心对称作图和平移作图,熟练掌握中心对称的性质和平移的性质是解答本题的关键. 中心对称的性质:①关于中心对称的两个图形能够完全重合;②关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分.
【题型】解答题
【结束】
22
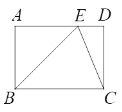
【题目】如图,在矩形ABCD中,点E在AD上,且EC平分∠BED.
(1)△BEC是否为等腰三角形?证明你的结论.
(2)已知AB=1,∠ABE=45°,求BC的长.
【答案】(1)见解析;(2)![]() .
.
【解析】(1)由矩形的性质和角平分线的定义得出∠DEC=∠ECB=∠BEC,推出BE=BC即可;
(2)求出AE=AB=1,根据勾股定理求出BE即可.
详解:(1) △BEC为等腰三角形
∵矩形ABCD,∴AD∥BC,
∴![]() =
= ![]() .
.
又∵![]() ,
,
![]() ,
,
![]() ,
,
∴△BEC为等腰三角形.
(2)∵矩形ABCD,
∴![]() .
.
又∵AB=1,∠ABE=45°∴由勾股定理得![]() =
=![]() ,
,
由(1)得![]() .
.

练习册系列答案
相关题目