题目内容
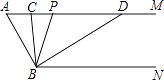
【题目】如下图。 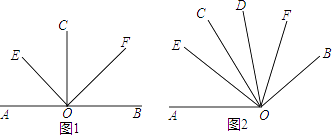
(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;
(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;
(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC= . (用含α与β的代数式表示)
【答案】
(1)解:∵CO⊥AB,
∴∠AOC=∠BOC=90°,
∵OE平分∠AOC,
∴∠EOC= ![]() ∠AOC=
∠AOC= ![]() ×90°=45°,
×90°=45°,
∵OF平分∠BOC,
∴∠COF= ![]() ∠BOC=
∠BOC= ![]() ×90°=45°,
×90°=45°,
∠EOF=∠EOC+∠COF=45°+45°=90°
(2)解:∵OE平分∠AOD,
∴∠EOD= ![]() ∠AOD=
∠AOD= ![]() ×(80+β)=40+
×(80+β)=40+ ![]() β,
β,
∵OF平分∠BOC,
∴∠COF= ![]() ∠BOC=
∠BOC= ![]() ×(80+β)=40+
×(80+β)=40+ ![]() β,
β,
∠COE=∠EOD﹣∠COD=40+ ![]() β﹣β=40﹣
β﹣β=40﹣ ![]() β;
β;
∠EOF=∠COE+∠COF=40﹣ ![]() β+40+
β+40+ ![]() β=80°
β=80°
(3)![]()
【解析】解:(3)如图2,∵∠AOC=∠BOD=α,∠COD=β, ∴∠AOD=α+β,
∵OE平分∠AOD,
∴∠DOE= ![]() (α+β),
(α+β),
∴∠COE=∠DOE﹣∠COD= ![]() =
= ![]() ,
,
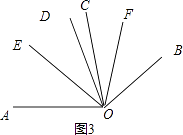
如图3,∵∠AOC=∠BOD=α,∠COD=β,
∴∠AOD=α+β,
∵OE平分∠AOD,
∴∠DOE= ![]() (α﹣β),
(α﹣β),
∴∠COE=∠DOE+∠COD= ![]() .
.
综上所述: ![]() ,
,
故答案为: ![]() .
.
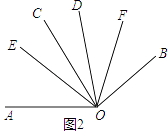
(1)根据垂直的定义得到∠AOC=∠OC=90°,根据角平分线的定义即可得到结论;(2)根据角平分线的定义得到∠EOD= ![]() ∠AOD=
∠AOD= ![]() ×(80+β)=40+
×(80+β)=40+ ![]() β,∠COF=
β,∠COF= ![]() ∠BOC=
∠BOC= ![]() ×(80+β)=40+
×(80+β)=40+ ![]() β,根据角的和差即可得到结论;(3)如图2由已知条件得到∠AOD=α+β,根据角平分线的定义得到∠DOE=
β,根据角的和差即可得到结论;(3)如图2由已知条件得到∠AOD=α+β,根据角平分线的定义得到∠DOE= ![]() (α+β),即可得到结论.
(α+β),即可得到结论.

【题目】某市在城中村改造中,需要种植A、B两种不同的树苗共3000棵,经招标,承包商以15万元的报价中标承包了这项工程,根据调查及相关资料表明,A、B两种树苗的成本价及成活率如表:
品种 | 购买价(元/棵) | 成活率 |
A | 28 | 90% |
B | 40 | 95% |
设种植A种树苗x棵,承包商获得的利润为y元.
(1)求y与x之间的函数关系式;
(2)政府要求栽植这批树苗的成活率不低于93%,承包商应如何选种树苗才能获得最大利润?最大利润是多少?
(3)在达到(2)中政府的要求并获得最大利润的前提下,承包商用绿化队的40人种植这两种树苗,已知每人每天可种植A种树苗6棵或B种树苗3棵,如何分配人数才能使种植A、B两种树苗同时完工.