题目内容
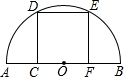 (2012•道孚县模拟)如图,在以AB为直径的半圆中,有一个边长为1的内接正方形CDEF,则以AC和BC的长为两根的一元二次方程是
(2012•道孚县模拟)如图,在以AB为直径的半圆中,有一个边长为1的内接正方形CDEF,则以AC和BC的长为两根的一元二次方程是此题答案不唯一,如:x2-
x+1=0.
| 5 |
此题答案不唯一,如:x2-
x+1=0.
.| 5 |
分析:连接AD,BD,OD,由AB为直径与四边形DCFE是正方形,即可证得△ACD∽△DCB,则可求得AC•BC=DC2=1,又由勾股定理求得AB的值,即可得AC+BC=AB,根据根与系数的关系即可求得答案.注意此题答案不唯一.
解答: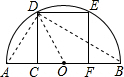 解:连接AD,BD,OD,
解:连接AD,BD,OD,
∵AB为直径,
∴∠ADB=90°,
∵四边形DCFE是正方形,
∴DC⊥AB,
∴∠ACD=∠DCB=90°,
∴∠ADC+∠CDB=∠A+∠ADC=90°,
∴∠A=∠CDB,
∴△ACD∽△DCB,
∴AC:DC=DC:BC,
又∵正方形CDEF的边长为1,
∵AC•BC=DC2=1,
∵AC+BC=AB,
在Rt△OCD中,OC2+CD2=OD2,
∴OD=
=
,
∴AC+BC=AB=2OD=
,
∴以AC和BC的长为两根的一元二次方程是x2-
x+1=0.
故答案为:此题答案不唯一,如:x2-
x+1=0.
 解:连接AD,BD,OD,
解:连接AD,BD,OD,∵AB为直径,
∴∠ADB=90°,
∵四边形DCFE是正方形,
∴DC⊥AB,
∴∠ACD=∠DCB=90°,
∴∠ADC+∠CDB=∠A+∠ADC=90°,
∴∠A=∠CDB,
∴△ACD∽△DCB,
∴AC:DC=DC:BC,
又∵正方形CDEF的边长为1,
∵AC•BC=DC2=1,
∵AC+BC=AB,
在Rt△OCD中,OC2+CD2=OD2,
∴OD=
12+(
|
| ||
| 2 |
∴AC+BC=AB=2OD=
| 5 |
∴以AC和BC的长为两根的一元二次方程是x2-
| 5 |
故答案为:此题答案不唯一,如:x2-
| 5 |
点评:此题考查了正方形的性质,相似三角形的判定与性质以及根与系数的关系.此题属于开放题,注意数形结合与方程思想的应用.

练习册系列答案
相关题目
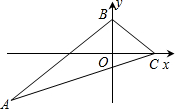 (2012•道孚县模拟)如图,△ABC的内心在y轴上,点C的坐标为(2,0),点B的坐标为(0,2),直线AC的解析式为:
(2012•道孚县模拟)如图,△ABC的内心在y轴上,点C的坐标为(2,0),点B的坐标为(0,2),直线AC的解析式为: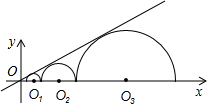 (2012•道孚县模拟)如图,三个半圆依次相外切,它们的圆心都在x轴上,并与直线y=
(2012•道孚县模拟)如图,三个半圆依次相外切,它们的圆心都在x轴上,并与直线y=