题目内容
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣3).
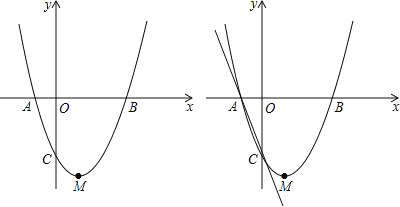
(1)求该抛物线的解析式及顶点M坐标;
(2)求△BCM面积与△ABC面积的比;
(3)若P是x轴上一个动点,过P作射线PQ∥AC交抛物线于点Q,随着P点的运动,在抛物线上是否存在这样的点Q,使以A,P,Q,C为顶点的四边形为平行四边形?若存在,请求出Q点坐标;若不存在,请说明理由.
【答案】(1)y=x2﹣2x﹣3=(x﹣1)2﹣4,M(1,﹣4).(2)S△BCM:S△ABC=3:6=1:2.(3)Q点为(2,﹣3)或(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3)
,3)
【解析】
试题分析:(1)有抛物线与x轴交于点A(﹣1,0),B(3,0)两点,则可设抛物线解析式为y=a(x+1)(x﹣3).由与y轴交于点C(0,﹣3),则代入易得解析式,顶点易知.
(2)求△BCM面积与△ABC面积的比,由两三角形不为同高或同底,所以考虑求解求出两三角形面积再作比即可.因为S△BCM=S梯形OCMD+S△BMD﹣S△BOC,S△ABC=![]() ABOC,则结论易得.
ABOC,则结论易得.
(3)由四边形为平行四边形,则对边PQ、AC平行且相等,过Q点作x轴的垂线易得Q到x轴的距离=OC=3,又(1)得抛物线解析式,代入即得Q点横坐标,则Q点可求.
解:(1)设抛物线解析式为y=a(x+1)(x﹣3),
∵抛物线过点(0,﹣3),
∴﹣3=a(0+1)(0﹣3),
∴a=1,
∴抛物线解析式为y=(x+1)(x﹣3)=x2﹣2x﹣3,
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴M(1,﹣4).
(2)如图1,连接BC、BM、CM,作MD⊥x轴于D,
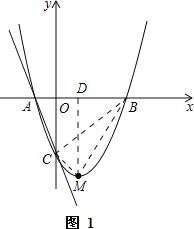
∵S△BCM=S梯形OCMD+S△BMD﹣S△BOC
=![]() (3+4)1+
(3+4)1+![]() 2×4﹣
2×4﹣![]() 33
33
=![]() +
+![]() ﹣
﹣![]() =3
=3
S△ABC=![]() ABOC=
ABOC=![]() 43=6,
43=6,
∴S△BCM:S△ABC=3:6=1:2.
(3)存在,理由如下:
①如图2,当Q在x轴下方时,作QE⊥x轴于E,
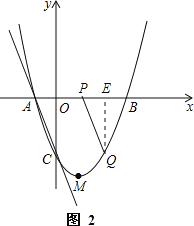
∵四边形ACQP为平行四边形,
∴PQ平行且相等AC,
∴△PEQ≌△AOC,
∴EQ=OC=3,
∴﹣3=x2﹣2x﹣3,
解得 x=2或x=0(与C点重合,舍去),
∴Q(2,﹣3).
②如图3,当Q在x轴上方时,作QF⊥x轴于F,

∵四边形ACPQ为平行四边形,
∴QP平行且相等AC,
∴△PFQ≌△AOC,
∴FQ=OC=3,
∴3=x2﹣2x﹣3,
解得 x=1+![]() 或x=1﹣
或x=1﹣![]() ,
,
∴Q(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3).
,3).
综上所述,Q点为(2,﹣3)或(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3)
,3)

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案