题目内容
【题目】如图，△ABC的中线AF与中位线DE相交于点O。
（1）AF与DE有怎样的关系？为什么？
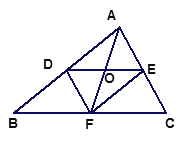
（2）当△ABC满足什么条件时，四边形DFEA是菱形？为什么？
【答案】(1) 互相平分 (2) （2）当△ABC是等腰三角形
【解析】试题分析：（1）由三角形中位线定理得到EF=AD，DF=AE，再由两组对边分别相等的四边形是平行四边形得到ADFE是平行四边形，由平行四边形对角线互相平分即可得到结论；
（2）当△ABC是等腰三角形时，证明AD=AE，由邻边相等的平行四边形是菱形即可得出结论．
试题解析：解：（1）AF与DE互相平分．理由如下：
由EF是△ABC的中位线，得EF=
AB．又AD=
AB，所以EF=AD．同样可得DF=AE．所以四边形ADFE是平行四边形，AF与DE互相平分．
（2）当△ABC是等腰三角形时，四边形ADFE是菱形．理由如下：
∵△ABC是等腰三角形，∴AB=AC．∵DE是△ABC的中位线，∴AD=AE，∴平行四边形ABCD是菱形．
练习册系列答案
相关题目
