题目内容
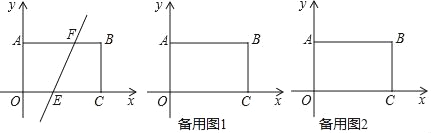
【题目】如图,在平面直角坐标系中,函数y=ax2+bx+c(a>0)的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),OB=OC,OC=3OA.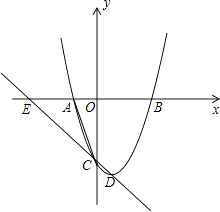
(1)求这个二次函数的表达式;
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度.
【答案】
(1)
解:∵点B的坐标为(3,0),OB=OC,
∴点C的坐标为(0,﹣3),
又∵OC=3OA,
∴OA=1,
∴点A的坐标为(﹣1,0),
将A、B、C三点坐标代入可得:  ,
,
解得: 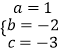 ,
,
故这个二次函数的表达式为:y=x2﹣2x﹣3
(2)
解:在该抛物线上存在点F(2,﹣3),使以点A、C、E、F为顶点的四边形为平行四边形.
理由:由(1)得D(1,﹣4),则直线CD的解析式为:y=﹣x﹣3,
故E点的坐标为(﹣3,0),
∵以A、C、E、F为顶点的四边形为平行四边形,
∴F点的坐标为(2,﹣3)或(﹣2,﹣3)或(﹣4,3),
代入抛物线的表达式检验,只有(2,﹣3)符合.
∴抛物线上存在点F(2,﹣3),使以点A、C、E、F为顶点的四边形为平行四边形
(3)
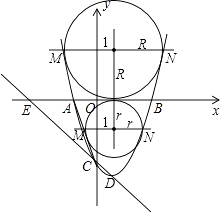
解:①如图,当直线MN在x轴上方时,设圆的半径为R(R>0),
则N(R+1,R),代入抛物线的表达式,解得R= ![]() ,
,
其中R= ![]() (不合题意,舍去),
(不合题意,舍去),
∴R= ![]() .
.
②如图,当直线MN在x轴下方时,设圆的半径为r(r>0),
则N(r+1,﹣r),
代入抛物线的表达式,解得:r= ![]() ,
,
其中r= ![]() (不合题意,舍去),
(不合题意,舍去),
∴r= ![]() .
.
综合①②得:圆的半径为 ![]() 或
或 ![]() .
.
【解析】(1)分别确定A、B、C的坐标,利用待定系数法可得二次函数的表达式;(2)根据A、C、E、F为顶点的四边形为平行四边形,可得点F的可能坐标,再由点F在抛物线上,可最终确定;(3)分两种情况讨论,①MN在x轴上,②MN在x轴下,表示出N的坐标,代入抛物线解析式可得半斤的长度.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 灵星计算小达人系列答案
灵星计算小达人系列答案