题目内容
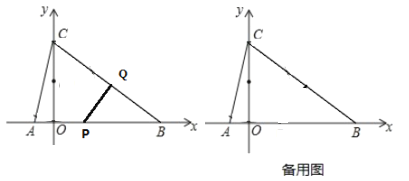
【题目】如图,在平面直角坐标系中,O是坐标原点,直线![]() 与x轴,y轴分别交于B,C两点,抛物线
与x轴,y轴分别交于B,C两点,抛物线![]() 经过B,C两点,与x轴的另一个交点为点A,动点P从点A出发沿AB以每秒3个单位长度的速度向点B运动,运动时间为t(0<t<5)秒.
经过B,C两点,与x轴的另一个交点为点A,动点P从点A出发沿AB以每秒3个单位长度的速度向点B运动,运动时间为t(0<t<5)秒.
(1)求抛物线的解析式及点A的坐标;
(2)在点P从点A出发的同时,动点Q从点B出发沿BC以每秒3个单位长度的速度向点C运动,动点N从点C出发沿CA以每秒![]() 个单位长度的速度向点A运动,运动时间和点P相同.
个单位长度的速度向点A运动,运动时间和点P相同.
①记△BPQ的面积为S,当t为何值时,S最大,最大值是多少?
②是否存在△NCQ为直角三角形的情形?若存在,求出相应的t值;若不存在,请说明理由.
【答案】(1)![]() A(-3,0);(2)
A(-3,0);(2)![]() 时,
时, ![]() . (3)t的值为
. (3)t的值为![]() 或
或![]() .
.
【解析】试题分析:(1)由直线y=![]() x+9与x轴,y轴分别交于B,C两点,分别令x=0和y=0求出B与C的坐标,又抛物线经过B,C两点,把求出的B与C的坐标代入到二次函数的表达式里得到关于b,c的方程,联立解出b和c即可求出二次函数的解析式.又因A点是二次函数与x轴的另一交点令y=0即可求出点A的坐标.
x+9与x轴,y轴分别交于B,C两点,分别令x=0和y=0求出B与C的坐标,又抛物线经过B,C两点,把求出的B与C的坐标代入到二次函数的表达式里得到关于b,c的方程,联立解出b和c即可求出二次函数的解析式.又因A点是二次函数与x轴的另一交点令y=0即可求出点A的坐标.
(2)连接OM,PM与⊙O′相切作为题中的已知条件来做.由直径所对的圆周角为直角可得∠OMC=90°从而得∠OMB=90°.又因为O′O是⊙O′的半径,O′O⊥OP得到OP为⊙O′的切线,然后根据从圆外一点引圆的两条切线,切线长相等可得OP=PM,根据等边对等角得∠POM=∠PMO,然后根据等角的余角相等可得∠PMB=∠OBM,再根据等角对等边得PM=PB,然后等量代换即可求出OP的长,加上OA的长即为点P运动过的路程AP,最后根据时间等于路程除以速度即可求出时间t的值.
(3)①由路程等于速度乘以时间可知点P走过的路程AP=3t,则BP=15-3t,点Q走过的路程为BQ=3t,然后aa过点Q作QD⊥OB于点D,证△BQD∽△BCO,由相似得比列即可表示出QD的长,然后根据三角形的面积公式即可得到S关于t的二次函数关系式,然后利用t=-![]() 时对应的S的值即可求出此时的最大值.
时对应的S的值即可求出此时的最大值.
②要使△NCQ为直角三角形,必须满足三角形中有一个直角,由BA=BC可知∠BCA=∠BAC,所以角NCQ不可能为直角,所以分两种情况来讨论:第一种,当角NQC为直角时,利用两组对应角的相等可证△NCQ∽△CAO,由相似得比例即可求出t的值;第二种当∠QNC=90°时,也是证三角形的相似,由相似得比例求出t的值.
试题解析:(1)在![]() 中,令x=0,得y=9;令y=0,得x=12.∴C(0,9),B(12,0).
中,令x=0,得y=9;令y=0,得x=12.∴C(0,9),B(12,0).
又抛物线经过B,C两点,∴![]() ,解得:
,解得: ![]() ,∴
,∴![]()
令y=0,解得:A(-3,0)
(2)①过点Q作QD⊥OB于点D.
∵OC⊥OB,∴QD∥OC.∴△BQD∽△BCO.∴ ![]()
∵OC=9,BQ=3t,BC=15,∴![]() ,解得
,解得![]()
又![]()
∴![]() (0<t<5)
(0<t<5)
当![]() 时,
时, ![]() .
.
②存在△NCQ为直角三角形的情形.
∵BC=BA=15, ∴∠BCA=∠BAC,即∠NCQ=∠CAO
∴△NCQ欲为直角三角形,∠NCQ≠90°,只存在∠NQC=90°和∠QNC=90°两种情况.
如图,当∠NQC=90°时,∠NQC=∠COA=90°,∠NCQ=∠CAO
∴△NQC∽△COA,∴ ![]() ,∴
,∴ ,解得:
,解得: ![]() ;
;
当∠QNC=90°时,∠QNC=∠COA=90°,∠NCQ=∠CAO
∴△NQC∽△OCA,∴ ![]() ,∴
,∴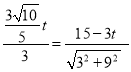 ,解得:t=
,解得:t=![]() .
.
综上,存在△NCQ为直角三角形的情形,t的值为![]() 或
或![]() .
.

 名校课堂系列答案
名校课堂系列答案