Question

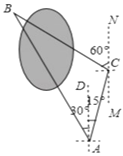
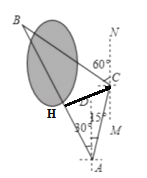
【题目】小明同学要测量公园内被湖水隔开的两颗大树A和B之间的距离，他在A处测得大树B在A的北偏西30°方向，他从A处出发向北偏东15°方向走了200米到达C处，测得大树B在C的北偏西60°的方向.

（1）求∠ABC的度数；

（2）求两棵大树A和B之间的距离（结果精确到1米；参考数据， ， ）.

Answer 1

【答案】两棵大树A和B之间的距离约为386米

【解析】试题分析：（1）先利用平行线的性质得∠ACM=∠DAC=15°，再利用平角的定义计算出∠ACB=105°，然后根据三角形内角和计算∠ABC的度数；
（2）作CH⊥AB于H，如图，易得△ACH为等腰直角三角形，则AH=CH=AC=100，在Rt△BCH中利用含30度的直角三角形三边的关系得到BH=CH=100，AB=AH+BH=100+100，然后进行近似计算即可．

试题解析：由题意可知：∠BAC=∠BAD+∠CAD=30°+15°=45°，∠MCA=∠CAD=15°，

∴∠ACB=180°-∠MCA-∠BCN=180°-15°-60°=105°

在△ABC中，∠ABC=180°-∠BCA-∠BAC=180°-105°-45°=30°；

从点C作CH⊥AB于点H

.

在Rt△ACH中，∵AC=200(米)，∠CAH=45°，

∴CH=ACsin∠CAH=200×sin45°=200×=100 （米）

∴AH=CH=100 (米)

在Rt△BCH中，∵CH=100 (米)，∠CBH=30°，

∴；

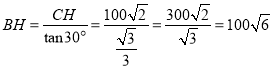∴AB=AH+BH=100+100≈386（米）

答：两棵大树A和B之间的距离约为386米