题目内容
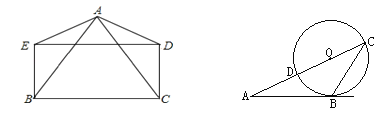
【题目】(1)已知:如图,四边形BCDE是矩形,AB=AC.求证:AE=AD
(2)如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B. 若∠A=30°,求∠C
【答案】(1)证明见解析;(2)30°.
【解析】
试题分析:(1)欲证明AE=AD,只要证明△ABE≌△ACD即可.
(2)如图2中,连接OB,根据∠C=![]() ∠AOB,求出∠AOB即可解决问题.
∠AOB,求出∠AOB即可解决问题.
试题解析:(1)如图1中,

∵四边形BCDE是矩形,
∴EB=DC,∠EBC=∠DCB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠EBA=∠DCA,
在△ABE和△ACD中,
 ,
,
∴△ABE≌△ACD,
∴AE=AD.
(2)如图2中,连接OB.

∵AB是⊙O切线,
∴OB⊥AB,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∴∠C=![]() ∠AOB=30°
∠AOB=30°

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目