题目内容
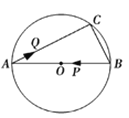
【题目】如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
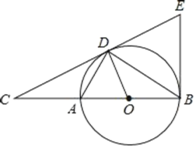
(1)判断直线CD和⊙O的位置关系,并说明理由;
(2)过点B作⊙O的切线BE交直线CD于点E,若BE=5,CD=8,求⊙O的半径.
【答案】(1)直线CD和⊙O的位置关系是相切,理由见解析;(2)⊙O的半径为![]() .
.
【解析】
(1)因为直径所对的圆周角是90°,所以∠ADB=90°,所以∠DAB+∠DBA=90°,
又因为OD=OA,所以得出∠DAB=∠ADO,之后进一步求解即可。
(2)根据CD是⊙O的切线,BE是⊙O的切线,所以得出DE=BE=5,∠CBE=90°=∠CDO,再利用勾股定理求出BC的长,进一步证明△COD∽△CEB,之后利用相似三角形性质求解即可。
(1)直线CD和⊙O的位置关系是相切,理由如下:
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠DBA=90°,
∵∠CDA=∠CBD,
∴∠DAB+∠CDA=90°,
∵OD=OA,
∴∠DAB=∠ADO,
∴∠CDA+∠ADO=90°,
即∠CDO=90°,
∴OD⊥CE,
∴直线CD是⊙O的切线;
(2)∵CD是⊙O的切线,BE是⊙O的切线,
∴DE=BE=5,∠CBE=90°=∠CDO,
∴CE=CD+DE=13,
∴BC=![]() =
=![]() ,
,
∵∠C=∠C,∴△COD∽△CEB,
∴![]() =
=![]() ,即
,即![]() ,
,
解得:OC=![]() ,
,
∴OB=BC﹣OC=![]() ,
,
即⊙O的半径为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目