题目内容
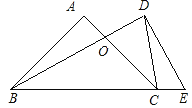
【题目】如图,在图(1)中,猜想:∠A+∠B+∠C+∠D+∠E+∠F=______度.
请说明你猜想的理由.
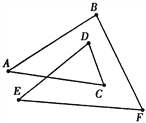
图1
如果把图1成为2环三角形,它的内角和为∠A+∠B+∠C+∠D+∠E+∠F;图2称为2环四边形,它的内角和为∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H;

图2
则2环四边形的内角和为_____________________________________________度;
2环五边形的内角和为________________________________________________度;
2环n边形的内角和为________________________________________________度.
【答案】(1)360°;(2)720°;(3)1080°;(4)2(n-2)×180°
【解析】解:连结BB1,则∠A1+∠C=∠BB1A1+∠B1BC,∠A+∠B+∠C+∠A1+∠B1+∠C1=∠A+∠ABB1+∠BB1C1+∠C1=360度,得到:2环三角形的内角和为360°;
2环四边形:如图,AA1之间添加两条边,可得B1+∠C1+∠D1=∠EAD+∠AEA1+∠EA1B1
则∠A+∠B+∠C+∠D+∠A1+∠B1+∠C1+∠D1=∠EAB+∠B+∠C+∠D+∠DA1E+∠E=720°,得到:2环四边形的内角和为720°;
2环五边形:如图,AA1之间添加三条边,同2换四边形可得:2环五边形的内角和为1080°;
二环n边形添加(n﹣2)条边,二环n边形的内角和成为(2n﹣2)边形的内角和.其内角和为180(2n﹣4)=360(n﹣2)度.
故答案为:360;720;1080;360(n﹣2).


练习册系列答案
相关题目