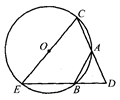
题目内容
如图,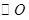 的直径
的直径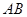 为10cm,弦
为10cm,弦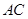 为6cm,
为6cm,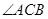 的平分线交
的平分线交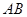 于
于 ,交
,交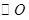 于
于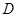 .求弦
.求弦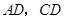 的长及
的长及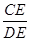 的值.
的值.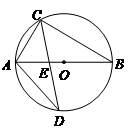
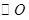 的直径
的直径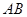 为10cm,弦
为10cm,弦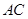 为6cm,
为6cm,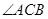 的平分线交
的平分线交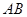 于
于 ,交
,交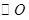 于
于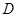 .求弦
.求弦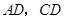 的长及
的长及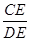 的值.
的值.
 ,
, ,
,
试题分析:连结
 ,过
,过 作
作 于
于 ,先根据圆周角定理可得∠ACB=90°,根据勾股定理求得BC的长,由CD平分∠ACB可得弧AD=弧BD,AD=BD,根据勾股定理即可求得AD、BD的长,在
,先根据圆周角定理可得∠ACB=90°,根据勾股定理求得BC的长,由CD平分∠ACB可得弧AD=弧BD,AD=BD,根据勾股定理即可求得AD、BD的长,在 中根据余弦函数的定义可得AM、CM的长,再根据勾股定理即可求得DM的长,从而得到CD的长,再证得
中根据余弦函数的定义可得AM、CM的长,再根据勾股定理即可求得DM的长,从而得到CD的长,再证得 ∽
∽ ,根据相似三角形的性质即可求得结果.
,根据相似三角形的性质即可求得结果.连结
 ,过
,过 作
作 于
于 ,
,
 是直径,
是直径,
在
 中,
中, (cm)
(cm) 平分
平分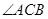 ,
, ,
,
在
 中,
中, (cm)
(cm)在
 中,
中,
在
 中 ,
中 ,
∴
 (cm)
(cm)∵
 ,
,
∴
 ∽
∽
∴

∴

∴

∴
 .
.点评:解答本题的根据是熟练掌握直径所对的圆周角是直角,相似三角形的对应边成比例,注意对应字母在对应位置上.

练习册系列答案
相关题目

 cm的弦AB,则弦AB所对的圆周角度数为( )
cm的弦AB,则弦AB所对的圆周角度数为( ) 

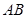 为⊙
为⊙ 的直径,
的直径,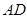 与⊙
与⊙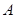 ,
,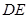 与⊙
与⊙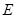 ,点
,点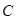 为
为
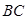 为⊙
为⊙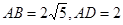 ,求线段BC和EG的长.
,求线段BC和EG的长.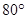 的圆心角所对的弧长是
的圆心角所对的弧长是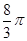 cm ,则该圆的半径为 cm .
cm ,则该圆的半径为 cm .