题目内容
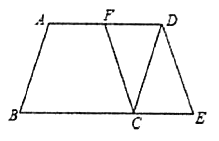
【题目】如图①,△ABC是等腰直角三角形,![]() ,
,![]() ,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时
,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时![]() ,
,![]() 成立.
成立.

(1)当△ABC绕点A逆时针旋转![]() 时,如图②,
时,如图②,![]() 成立吗?若成立,请证明;若不成立,请说明理由;
成立吗?若成立,请证明;若不成立,请说明理由;
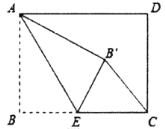
(2)当△ABC绕点A逆时针旋转45°时,如图③,延长DB交CF于点H;
(i)求证:![]() ;
;
(ii)当![]() ,
,![]() 时,则线段FC的长为_______.
时,则线段FC的长为_______.
【答案】(1)BD=CF成立,理由见解析;(2)(i)证明见解析;(ii)2.
【解析】
(l)由旋转得:AB=AC,∠CAF=∠BAD=α,AD=AF,由SAS证得△ABD≌△ACF,即可得出结论;
(2)(i)由△ABD≌△ACF,得出∠HFN=∠ADN,证得∠HFN+∠HNF=90°,得出∠NHF=90°,即可得出结论;
(ii)由正方形的性质得出AF=AD=![]() +1,∠DAF=90°,AD⊥AF,由等腰直角三角形的性质得出∠ABC=45°,BC=
+1,∠DAF=90°,AD⊥AF,由等腰直角三角形的性质得出∠ABC=45°,BC=![]() AB=2,由旋转的性质得:∠BAD=45°=∠ABC,得出BC∥AD,证出BC⊥AF,由等腰三角形的性质得出AP=BP=CP=
AB=2,由旋转的性质得:∠BAD=45°=∠ABC,得出BC∥AD,证出BC⊥AF,由等腰三角形的性质得出AP=BP=CP=![]() BC=1,得出PF=AFAP=
BC=1,得出PF=AFAP=![]() ,由勾股定理即可得出结果.
,由勾股定理即可得出结果.
解:(l)BD=CF成立;
理由如下:
由旋转得:AB=AC,∠CAF=∠BAD=α,AD=AF,
在△ABD和△ACF中,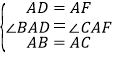 ,
,
∴△ABD≌△ACF(SAS),
∴BD=CF;
(2)(i)证明:由(1)得,△ABD≌△ACF,
∴∠HFN=∠ADN,
∵∠HNF=∠AND,∠AND+∠ADN=90°,
∴∠HFN+∠HNF=90°,
∴∠NHF=90°,
∴HD⊥HF,即BD⊥CF;
(ii)解:∵四边形ADEF是正方形,
∴AF=AD=![]() +1,∠DAF=90°,AD⊥AF,
+1,∠DAF=90°,AD⊥AF,
∵△ABC是等腰直角三角形,∠BAC=90°,AB=AC,
∴∠ABC=45°,BC=![]() AB=2,
AB=2,
由旋转的性质得:∠BAD=45°=∠ABC,
∴BC∥AD,
∴BC⊥AF,
∴AP=BP=CP=![]() BC=1,
BC=1,
∴PF=AFAP=![]() ,
,
∴FC=![]() .
.