Question

【题目】如图，在△ABC中，∠ABC=100°，∠ACB=40°，∠ABC的平分线BD交AC于点D，∠ACB的平分线CP交BD于点D．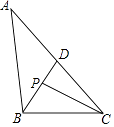

（1）BD与AC的位置关系是 ．
（2）求∠BPC的度数．

Answer 1

【答案】
（1）互相垂直
（2）解：∵PC平分∠ACB，∠ACB=40°，

∴∠BCP= ∠ACB=20°，

∴∠BPC=180°﹣∠PBC﹣∠BCP=180°﹣50°﹣20°=110°

【解析】解：（1）∵∠ABC=100°，BD平分∠ABC，

∴∠DBC= ∠ABC=50°，

∴∠BDC=180°﹣∠DBC﹣∠BCD=90°，

∴BD⊥AC．

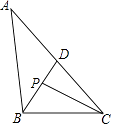
（2）∵PC平分∠ACB，∠ACB=40°，

∴∠BCP= ∠ACB=20°，

∴∠BPC=180°﹣∠PBC﹣∠BCP=180°﹣50°﹣20°=110°

所以答案是：（1）互相垂直；（2）110°.
【考点精析】根据题目的已知条件，利用三角形的内角和外角的相关知识可以得到问题的答案，需要掌握三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角．