题目内容
如图,在平面直角坐标系xOy中,一次函数y1=-
x+2与x轴、y轴分别相交于点A和点B,直线y2=kx+b(k≠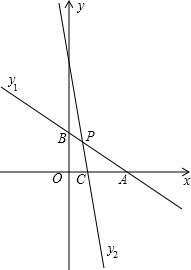 0)经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
0)经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
(1)求△ABO的面积;
(2)若△ABO被直线CP分成的两部分的面积相等,求点P的坐标及直线CP的函数表达式.
| 2 |
| 3 |
 0)经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
0)经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.(1)求△ABO的面积;
(2)若△ABO被直线CP分成的两部分的面积相等,求点P的坐标及直线CP的函数表达式.
(1)在直线y1=-
x+2中,令x=0,得y1=2,
∴B(0,2),
令y1=0,得x=3,
∴A(3,0),
∴S△ABO=
AO•BO=
×3×2=3;
(2)
S△ABO=
×3=
,
∵点P在第一象限,
∴S△APC=
AC•yp=
×(3-1)×yp=
,
解得yp=
,
而点P又在直线y1上,
∴
=-
x+2,
解得x=
,
∴P(
,
),
将点C(1,0)、P(
,
),代入y=kx+b中,有
,
∴
.
∴直线CP的函数表达式为y=-6x+6.
| 2 |
| 3 |
∴B(0,2),

令y1=0,得x=3,
∴A(3,0),
∴S△ABO=
| 1 |
| 2 |
| 1 |
| 2 |
(2)
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∵点P在第一象限,
∴S△APC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解得yp=
| 3 |
| 2 |
而点P又在直线y1上,
∴
| 3 |
| 2 |
| 2 |
| 3 |
解得x=
| 3 |
| 4 |
∴P(
| 3 |
| 4 |
| 3 |
| 2 |
将点C(1,0)、P(
| 3 |
| 4 |
| 3 |
| 2 |
|
∴
|
∴直线CP的函数表达式为y=-6x+6.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
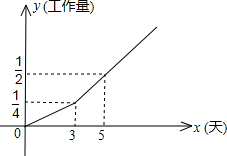 修3天,剩下的工作由甲,乙两个装修公路合作完成.工程进度满足如图所示的函数关系,该家庭共支付工资8000元.
修3天,剩下的工作由甲,乙两个装修公路合作完成.工程进度满足如图所示的函数关系,该家庭共支付工资8000元.

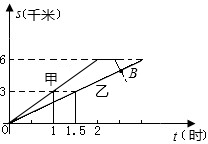 路程随时间变化关系如图所示:
路程随时间变化关系如图所示: