题目内容
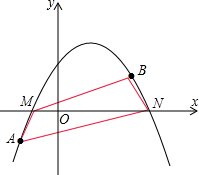
已知抛物线y=ax2+bx+c(a≠0)经过A(-2,-3)、B(3,2)两点,且与x轴相交于M、N两点,当以线段MN为直径的圆的面积最小时,求M、N两点的坐标和四边形AMBN的面积.
由抛物线经过A(-2,-3)、B(3,2)两点可得b=1-a,c=-(1+6a)
∴MN=丨x1-x2丨=|
|=|±
|=
=
.
当a=-1时,MN最小=2
此时,b=2,c=5,
∴函数的解析式为:y=-x2+2x+5.
∴M(1-
,0),N(1+
,0),
此时,四边形AMBN的面积S=
MN•(|yA|+|yB|)=
×2
×(3+2)=5
.
∴MN=丨x1-x2丨=|
| ||
| a |
|
(
|
(
|
当a=-1时,MN最小=2
| 6 |
此时,b=2,c=5,
∴函数的解析式为:y=-x2+2x+5.
∴M(1-
| 6 |
| 6 |
此时,四边形AMBN的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| 6 |


练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目



 竹篱笆围成,竹篱笆的长为40m,读九年级的儿子小军为他设计了如下方案:如图,把养鸡场围成等腰梯形ABCD,且∠ABC=120°.
竹篱笆围成,竹篱笆的长为40m,读九年级的儿子小军为他设计了如下方案:如图,把养鸡场围成等腰梯形ABCD,且∠ABC=120°.