��Ŀ����
һ�ҵ��Թ�˾�Ƴ�һ�����͵��ԣ�Ͷ���г�������ǰ�����µ����������ͼ��ʾ����ͼ���Խ��Ƶؿ��������ߵ�һ���֣����е�x�µ�����Ϊy��Ԫ������y��x����Ĺ�ϵ���䣮����ͼ�����������⣺
��1���������߶�Ӧ�Ķ��κ�������ʽ��
��2���ù�˾�ھ�Ӫ�˿���ԵĹ����У��ڼ��µ����������������Ƕ��٣�
��3����˾���㣬���������½���ʼ��ÿ�¶����µ����۶����Ԥ�⣬����������µ��������10��Ԫ�������¾�ֹͣ���۸ò�Ʒ������Ԥ��ò�Ʒ�������۵�������

��1���������߶�Ӧ�Ķ��κ�������ʽ��
��2���ù�˾�ھ�Ӫ�˿���ԵĹ����У��ڼ��µ����������������Ƕ��٣�
��3����˾���㣬���������½���ʼ��ÿ�¶����µ����۶����Ԥ�⣬����������µ��������10��Ԫ�������¾�ֹͣ���۸ò�Ʒ������Ԥ��ò�Ʒ�������۵�������

��1���߽�϶��κ���ͼ��ó�ͼ���ϵĵ��У�
��1��13������2��24������0��0��
����y=ax2+bx+c�ã�
��ã�
���Խ���ʽΪ��y=-x2+14x
��2����y=-x2+14x=-��x-7��2+49
�𣺵�7�µ�����������������49��Ԫ��
��3�����x�µ���������µ��������10��Ԫ��
����֪�ã�-x2+14x+��x+1��2-14��x+1����10
2x-13��10��x��11.5����x=11ʱ��y=33��
��x=12ʱ��y=24����x=13ʱ��y=13��
��Ԥ��ò�Ʒ�������۵�ʱ����12���£�
��1��13������2��24������0��0��
����y=ax2+bx+c�ã�
|
��ã�
|
���Խ���ʽΪ��y=-x2+14x
��2����y=-x2+14x=-��x-7��2+49
�𣺵�7�µ�����������������49��Ԫ��
��3�����x�µ���������µ��������10��Ԫ��
����֪�ã�-x2+14x+��x+1��2-14��x+1����10
2x-13��10��x��11.5����x=11ʱ��y=33��
��x=12ʱ��y=24����x=13ʱ��y=13��
��Ԥ��ò�Ʒ�������۵�ʱ����12���£�

��ϰ��ϵ�д�
�����Ŀ
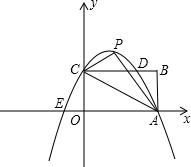
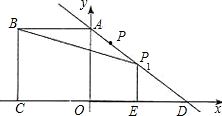 ��BCEP1�����ΪS������S�Ƿ������ֵ�����У������P�������S�����ֵ����û�У���˵�����ɣ�
��BCEP1�����ΪS������S�Ƿ������ֵ�����У������P�������S�����ֵ����û�У���˵�����ɣ�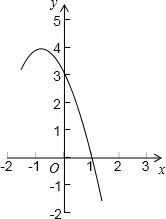
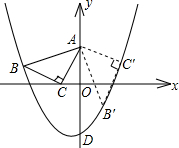 �е�A��y���ϣ���B��������y=ax2+ax-2�ϣ���C������Ϊ��-1��0����
�е�A��y���ϣ���B��������y=ax2+ax-2�ϣ���C������Ϊ��-1��0���� ����OEƽ�У�����������ÿ��
����OEƽ�У�����������ÿ��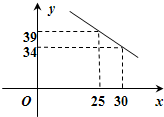 4��Ԫ���������ʽ�ȫ�����������������ͺŵ������������ͺŵ����������ɱ����ۼ����±���
4��Ԫ���������ʽ�ȫ�����������������ͺŵ������������ͺŵ����������ɱ����ۼ����±���