题目内容
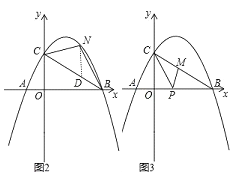
【题目】如图1，抛物线y=﹣
[（x﹣2）2+n]与x轴交于点A（m﹣2，0）和B（2m+3，0）（点A在点B的左侧），与y轴交于点C，连结BC．
（1）求m、n的值；
（2）如图2，点N为抛物线上的一动点，且位于直线BC上方，连接CN、BN．求△NBC面积的最大值；
（3）如图3，点M、P分别为线段BC和线段OB上的动点，连接PM、PC，是否存在这样的点P，使△PCM为等腰三角形，△PMB为直角三角形同时成立？若存在，求出点P的坐标；若不存在，请说明理由．
【答案】(1)m=1，n=﹣9；(2)
；(3)存在，P点坐标为（
，0）或（
，0）．
【解析】
试题分析：（1）利用抛物线的解析式确定对称轴为直线x=2，再利用对称性得到2﹣（m﹣2）=2m+3﹣2，解方程可得m的值，从而得到A（﹣1，0），B（5，0），然后把A点坐标代入y=﹣
[（x﹣2）2+n]可求出n的值；（2）作ND∥y轴交BC于D，如图2，利用抛物线解析式确定C（0，3），再利用待定系数法求出直线BC的解析式为y=﹣x+3，设N（x，﹣x2+
x+3），则D（x，﹣x+3），根据三角形面积公式，利用S△NBC=S△NDC+S△NDB可得S△BCN=﹣
x2+
x，然后利用二次函数的性质求解；（3）先利用勾股定理计算出BC=
，再分类讨论：当∠PMB=90°，则∠PMC=90°，△PMC为等腰直角三角形，MP=MC，设PM=t，则CM=t，MB=
﹣t，证明△BMP∽△BOC，利用相似比可求出BP的长，再计算OP后可得到P点坐标；当∠MPB=90°，则MP=MC，设PM=t，则CM=t，MB=﹣t，证明△BMP∽△BCO，利用相似比可求出BP的长，再计算OP后可得到P点坐标．
试题解析：（1）∵抛物线的解析式为y=﹣ [（x﹣2）2+n]=﹣（x﹣2）2﹣n，
∴抛物线的对称轴为直线x=2，
∵点A和点B为对称点，
∴2﹣（m﹣2）=2m+3﹣2，解得m=1，
∴A（﹣1，0），B（5，0），
把A（﹣1，0）代入y=﹣ [（x﹣2）2+n]得9+n=0，解得n=﹣9；
（2）作ND∥y轴交BC于D，如图2，
抛物线解析式为y=﹣ [（x﹣2）2﹣9]=﹣x2+
x+3，
当x=0时，y=3，则C（0，3），
设直线BC的解析式为y=kx+b，
把B（5，0），C（0，3）代入得
，解得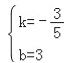
，
∴直线BC的解析式为y=﹣x+3，
设N（x，﹣x2+x+3），则D（x，﹣x+3），
∴ND=﹣x2+x+3﹣（﹣x+3）=﹣x2+3x，
∴S△NBC=S△NDC+S△NDB=
5ND=﹣
x2+
x=﹣（x﹣
）2+
，
当x=
时，△NBC面积最大，最大值为；
（3）存在．
∵B（5，0），C（0，3），
∴由勾股定理得BC=，
当∠PMB=90°，则∠PMC=90°，△PMC为等腰直角三角形，MP=MC，
设PM=t，则CM=t，MB=﹣t，
∵∠MBP=∠OBC，
∴△BMP∽△BOC，
∴
，即
，解得t=
，BP=
，
∴OP=OB﹣BP=5﹣
=
，
此时P点坐标为（，0）；
当∠MPB=90°，则MP=MC，
设PM=t，则CM=t，MB=﹣t，
∵∠MBP=∠CBO，
∴△BMP∽△BCO，
∴
，即
，解得t=
，BP=
，
∴OP=OB﹣BP=5﹣=，
此时P点坐标为（，0）；
综上所述，P点坐标为（，0）或（
，0）．
