题目内容
【题目】如图,在矩形ABCD中,点E为边AB上一点,且AE=![]() AB,EF⊥EC,连接BF.
AB,EF⊥EC,连接BF.
(1)求证:△AEF∽△BCE;
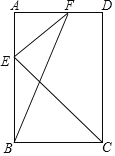
(2)若AB=3![]() ,BC=3,求线段FB的长.
,BC=3,求线段FB的长.
【答案】(1)证明见解析(2)![]()
【解析】分析:(1)、根据矩形的性质以及EF⊥EC得出∠AFE=∠BEC,从而得出三角形相似;(2)、根据题意得出AE和BE的长度,然后根据三角形相似得出AF的长度,然后根据Rt△ABF的勾股定理得出答案.
详解:(1)∵四边形ABCD是矩形, ∴∠A=∠CBE=90°, ∴∠AEF+∠AFE=90°,
又∵EF⊥EC, ∴∠AEF+∠BEC=90°, ∴∠AFE=∠BEC, ∴△AEF∽△BCE;
(2)∵AB=3![]() 、AE=
、AE=![]() AB, ∴AE=
AB, ∴AE=![]() 、BE=2
、BE=2![]() , ∵△AEF∽△BCE,
, ∵△AEF∽△BCE,
∴![]() =
=![]() ,即
,即![]() =
=![]() , 解得:AF=2, 则BF=
, 解得:AF=2, 则BF=![]() =
=![]() =
=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某学校党支部组织该校的6个党小组进行《新党章》知识竞赛活动,共设20道选择题,各题得分相同,每题必答.下表是6个党小组的得分情况:
党小组 | 答对题数 | 答错题数 | 得分 |
第一组 | 16 | 4 | 72 |
第二组 | 20 | 0 | 100 |
第三组 | 19 | 1 | 93 |
第四组 | 18 | 2 | 86 |
第五组 | 79 | ||
第六组 | 90? |
(1)根据表格数据可知,答对一题得_____分,答错一题得_______分;
(2)如第五组得79分,求出第五组答对题数是多少(用方程作答)?
(3)第六组组长说他们组得90分.你认为可能吗?为什么?