题目内容
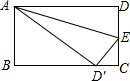
如图，已知正方形ABCD边长为10cm，点M从C到D以1cm/s的速度运动．将正方形ABCD折叠，使顶点A与点M重合，
折痕交AD于E，交BC于F，边AB折叠后与BC边交于点G．设点M的运动时间为t（0＜t＜10），单位：s．
（1）求证：△DEM∽△CMG；
（2）当t=5s时，求△DEM的周长；
（3）当5＜t＜10时，求△CMG的周长．
折痕交AD于E，交BC于F，边AB折叠后与BC边交于点G．设点M的运动时间为t（0＜t＜10），单位：s．（1）求证：△DEM∽△CMG；
（2）当t=5s时，求△DEM的周长；
（3）当5＜t＜10时，求△CMG的周长．
（1）根据折叠的性质知：∠EMG=∠A=90°
∴∠DME+∠CMG=90°
∵∠DME+∠DEM=90°
∴∠DEM=∠CMG
∵∠D=∠C=90°
∴△DEM∽△CMG．
（2）根据折叠的性质知：EM=EA，当t=5时，DM=CM=5
∴△DEM的周长为：DM+DE+EM=DM+DE+EA=DM+DA=15cm；
（3）依题意得：CM=t，DM=10-t，
设EM=EA=x，则DE=10-x
在Rt△DEM中，EM2=DE2+DM2，
即x2=（10-x）2+（10-t）2
解得：x=10-t+
，DE=10-x=t-
∵△DEM∽△CMG
∴
=
即
=
，
解得：GM=
同理可得：CG=
∴△CMG的周长为：CM+CG+MG=20cm．
∴∠DME+∠CMG=90°
∵∠DME+∠DEM=90°
∴∠DEM=∠CMG
∵∠D=∠C=90°
∴△DEM∽△CMG．
（2）根据折叠的性质知：EM=EA，当t=5时，DM=CM=5
∴△DEM的周长为：DM+DE+EM=DM+DE+EA=DM+DA=15cm；
（3）依题意得：CM=t，DM=10-t，
设EM=EA=x，则DE=10-x
在Rt△DEM中，EM2=DE2+DM2，
即x2=（10-x）2+（10-t）2
解得：x=10-t+
| t2 |
| 20 |
| t2 |
| 20 |
∵△DEM∽△CMG
∴
| ME |
| DE |
| GM |
| CM |
即
| x |
| 10-t |
| GM |
| t |
解得：GM=
| 200-20t+t2 |
| 20-t |
同理可得：CG=
| 200-20t |
| 20-t |
∴△CMG的周长为：CM+CG+MG=20cm．
练习册系列答案
相关题目
