题目内容
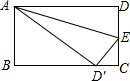
如图是一张直角三角形的纸片．两直角边AC=6cm，BC=8cm将△ABC折叠，使点B与点A重合，折痕为DE，则AD的长为（ ）
A．
| B．10cm | C．
| D．5cm |
设AD=xcm，
由折叠的性质得：BD=AD=xcm，
∵在Rt△ABC中，AC=6cm，BC=8cm，
∴CD=BC-BD=8-x（cm），
在Rt△ACD中，AC2+CD2=AD2，
即：62+（8-x）2=x2，
解得：x=
，
∴AD=
cm．
故选A．
由折叠的性质得：BD=AD=xcm，
∵在Rt△ABC中，AC=6cm，BC=8cm，
∴CD=BC-BD=8-x（cm），
在Rt△ACD中，AC2+CD2=AD2，
即：62+（8-x）2=x2，
解得：x=
| 25 |
| 4 |
∴AD=
| 25 |
| 4 |
故选A．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
