Question

【题目】对于平面直角坐标系中的任意两点P1（x1 ， y1），P2（x2 ， y2），我们把|x1﹣x2|+|y1﹣y2|叫做P1、P2两点间的直角距离，记作d（P1 ， P2）．
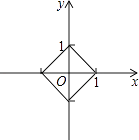
（1）已知O为坐标原点，动点P（x，y）满足d（O，P）=1，请写出x与y之间满足的关系式，并在所给的直角坐标系中画出所有符合条件的点P所组成的图形；
（2）设P0（x0 ， y0）是一定点，Q（x，y）是直线y=ax+b上的动点，我们把d（P0 ， Q）的最小值叫做P0到直线y=ax+b的直角距离．试求点M（2，1）到直线y=x+2的直角距离．

Answer 1

【答案】
（1）

解：由题意，得|x|+|y|=1，

∵d（O，P）=1，O（0，0），P（x，y）

∴d（0，P）=|x|+|y|

∴|x|+|y|=1

①x≥0，y≥0

∴x+y=1

y=1﹣x

②x≤0，y≤0

∴﹣x﹣y=1

y=﹣x﹣1

③x≥0，y≤0

∴x﹣y=1

y=x﹣1

④x≤0，y≥0

∴﹣x+y=1

y=1+x

将四个函数关系式表示在数轴上，所有符合条件的点P组成的图形如图所示：

（2）

解：∵d（M，Q）=|x﹣2|+|y﹣1|=|x﹣2|+|x+2﹣1|=|x﹣2|+|x+1|，

又∵x可取一切实数，|x﹣2|+|x+1|表示数轴上实数x所对应的点到数2和﹣1所对应的点的距离之和，其最小值为3．

∴点M（2，1）到直线y=x+2的直角距离为3

【解析】（1）根据新的运算规则知|x|+|y|=1，据此可以画出符合题意的图形；（2）根据新的运算规则知d（M，Q）=|x﹣2|+|y﹣1|=|x﹣2|+|x+2﹣1|=|x﹣2|+|x+1|，然后由绝对值与数轴的关系可知，|x﹣2|+|x+1|表示数轴上实数x所对应的点到数2和﹣1所对应的点的距离之和，其最小值为3．
【考点精析】利用绝对值对题目进行判断即可得到答案，需要熟知正数的绝对值是其本身，0的绝对值是0，负数的绝对值是它的相反数；注意：绝对值的意义是数轴上表示某数的点离开原点的距离．