题目内容
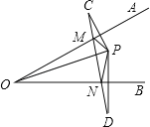
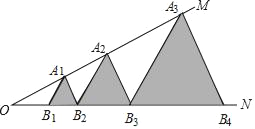
【题目】如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1B2、△A2B2B3、△A3B3B4、…均为等边三角形,若OB1=1,则△A8B8B9的边长为_____
【答案】128
【解析】
由等边三角形的性质可证得B2A1⊥OA1,再根据30°角所对的直角边是斜边的一半可求得B2A1= ![]() OB2,依此类推可求得答案.
OB2,依此类推可求得答案.
∵△B1A1B2为等边三角形,
∴∠A1B1B2=60°,
∵∠MON=30°,
∴∠OA1B2=30°+60°=90°,
∴B2A1=![]() OB2,
OB2,
同理可求得:A4B5=![]() OB5,
OB5,
∵OB1=1,
∴OB4=2OB3=4OB2=8OB1=8,OB5=2OB4=4OB3=8OB2=16OB1=16,
∴B4B5=OB5OB4=168=8,
以此类推: B8B9=128
故答案为128.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目