题目内容
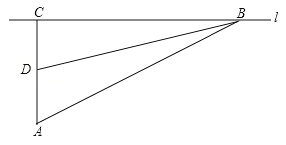
【题目】如图,∠AOB=30°,P是∠AOB内的一点,且OP=4cm,C、D分别是P关于OA、OB的对称点,连结CD、PM、PN,则△PMN的周长为________.
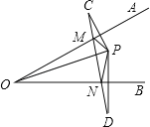
【答案】4cm
【解析】
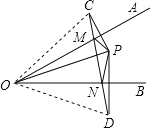
如图,连接OC、OD,先根据轴对称的性质得出OC=OD=OP,∠COD=2∠AOB=60°,进一步即可判定△OCD是等边三角形,从而可得CD=OC,而易证CD的长就是△PMN的周长,于是问题得解.
解:如图,连接OC、OD,∵C、D分别是点P关于OA、OB的对称点,
∴PM=CM、PN=DN,OC=OD=OP,∠AOP=∠AOC,∠BOP=∠BOD,
∵∠AOB=30°,
∴∠COD=∠AOC+∠AOP+∠BOD+∠BOP=2∠AOB=2×30°=60°,
∴△OCD是等边三角形,
∵OP=4cm,
∴CD=OC=4cm,
∴△PMN的周长=PM+MN+PN=CM+MN+ND=CD=4cm.
故答案为:4cm.

练习册系列答案
相关题目