Question

【题目】已知，在中，弦，连接、；

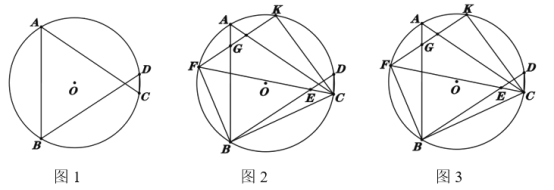
（1）如图1，求证：；

（2）如图2，在线段上取点，连接并延长交于点，交于点，，连接、、，，求的正切值；

（3）如图3，在（2）的条件下，交于点，，，求线段的长．

Answer 1

【答案】（1）见解析；（2）tan∠BCF=；（3）

【解析】

（1）根据平行线的性质可得∠B=∠D，然后根据圆的基本性质可得，然后根据等式的基本性质即可证出，最后根据圆的基本性质即可求出结论；

（2）过点K作KH⊥CD交CD的延长线于H，连接KD，根据等弧所对的圆周角相等可证∠BCF=∠DCK,从而得出tan∠BCF=tan∠DCK，设CK=5a，则DK=a，然后根据圆内接四边形的性质、等腰直角三角形的性质、锐角三角函数和勾股定理即可求出tan∠DCK，从而求出结论；

（3）在（2）的图上延长FK和CH，交于点M，用含a的式子求出CK、BF和KH，然后证出△CKM∽△CBF，最后列出比例式即可求出结论．

解：（1）∵

∴∠B=∠D

∴

∴

∴

∴；

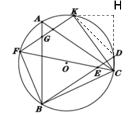
（2）过点K作KH⊥CD交CD的延长线于H，连接KD，

∵

∴，∠KFC=∠BEF=45°

∴BF=DK，∠BCF=∠DCK

∴tan∠BCF=tan∠DCK

∵，∠HDK为圆内接四边形CDKF的外角

∴，∠HDK=∠KFC=45°

∴△DKH为等腰直角三角形

设CK=5a，则DK=a，

∴DH=HK=DK·sin∠HDK=3a

在Rt△CKH中，CH=a

∴tan∠DCK=

∴tan∠BCF=

（3）在（2）的图上延长FK和CH，交于点M

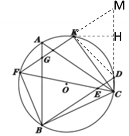
由（2）知：CK=5a，DH=HK=3a， BF=DK=a，∠BCF=∠DCK

∵CD∥AB，FK∥BD

∴四边形GBDM为平行四边形

∴BG=DM

∵=5a

∴DM=5a

∴MH=DM－DH=2a

在Rt△MKH中，KM=

∵∠CKM为圆内接四边形FBCK的外角

∴∠CKM=∠CBF

∴△CKM∽△CBF

∴

即

解得：a=

∴CK=5×=