Question

【题目】已知在平面直角坐标系中放置了5个如图所示的正方形（用阴影表示），点B1在y轴上，点C1、E1、E2、C2、E3、E4、C3在x轴上．若正方形A1B1C1D1的边长为1，∠B1C1O=60°，B1C1∥B2C2∥B3C3 ， 则点A3到x轴的距离是（ ）
A.
B.
C.
D.

Answer 1

【答案】D
【解析】解：过小正方形的一个顶点W作FQ⊥x轴于点Q，过点A3F⊥FQ于点F， ∵正方形A1B1C1D1的边长为1，∠B1C1O=60°，B1C1∥B2C2∥B3C3 ，
∴∠B3C3 E4=60°，∠D1C1E1=30°，∠E2B2C2=30°，
∴D1E1= D1C1= ，
∴D1E1=B2E2= ，
∴cos30°= = ，
解得：B2C2= ，
∴B3E4= ，
cos30°= ，
解得：B3C3= ，
则WC3= ，
根据题意得出：∠WC3 Q=30°，∠C3 WQ=60°，∠A3 WF=30°，
∴WQ= × = ，
FW=WA3cos30°= × = ，
则点A3到x轴的距离是：FW+WQ= + = ，
故选：D．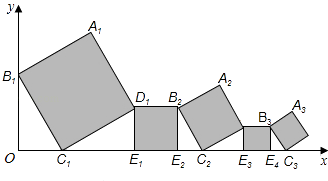

【考点精析】关于本题考查的正方形的性质和解直角三角形，需要了解正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)才能得出正确答案．