题目内容
已知：如图，四边形ABCD是⊙O的内接四边形，A是弧BD的中点，过A点的切线与CB的延长线交于点E．（1）求证：AB•DA=CD•BE；
（2）若点E在CB延长线上运动，点A在弧BD上运动，使切线EA变为割线EFA，其它条件不
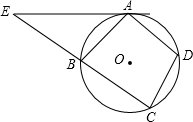变，问具备什么条件使原结论成立？（要求画出示意图，注明条件，不要求证明）
分析：（1）点A是弧BD的中点，根据弦切角定理和圆周角定理知∠1=∠3，由圆内接四边形的性质知∠ABE=∠D，于是有△ABE∽△CDA?
=
?AB•DA=CD•BE；
（2）要使结论仍然成立，则应有△ABE∽△CDA，故可使
=
．当
=
时有∠EAB=∠ACD，而由圆内接四边形的性质知∠ABE=∠ADC，故有△ABE∽△CDA，得
=
?AB•DA=CD•BE
| AB |
| CD |
| BE |
| DA |
（2）要使结论仍然成立，则应有△ABE∽△CDA，故可使
 |
| BF |
|
| DA |
|
| BF |
|
| DA |
| AB |
| CD |
| BE |
| DA |
解答：
（1）证明：连接AC
∵A是
的中点，
∴
=
．
∵EA切⊙O于点A，点C在⊙O上，
∴∠1=∠3=∠2
∵四边形ABCD是⊙O的内接四边形，
∴∠ABE=∠D
∴△ABE∽△CDA
∴
=
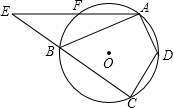
∴AB•DA=CD•BE．
（2）解：
如图，具备条件
=
（BF=DA，或∠BCF=∠DCA，或∠BAF=∠DCA，或FA∥BD等），使原结论成立
（1）证明：连接AC∵A是
|
| BD |
∴
|
| AB |
|
| AD |
∵EA切⊙O于点A，点C在⊙O上，
∴∠1=∠3=∠2
∵四边形ABCD是⊙O的内接四边形，
∴∠ABE=∠D
∴△ABE∽△CDA
∴
| AB |
| CD |
| BE |
| DA |
∴AB•DA=CD•BE．
（2）解：
如图，具备条件
|
| BF |
|
| DA |
点评：本题利用了弦切角定理、圆周角定理、相似三角形的判定和性质求解．
练习册系列答案
相关题目
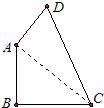已知，如图，四边形ABCD中∠B=90°，AB=9，BC=12，AD=8，CD=17．
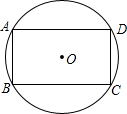已知：如图，四边形ABCD内接于⊙O，且AB∥CD，AD∥BC，
已知，如图，四边形ABCD是正方形，E、F分别是AB和AD延长线上的点，且BE=DF
已知：如图，四边形ABCD中，BC=CD=10，AB=15，AB⊥BC，CD⊥BC，若把四边形ABCD绕直线AB旋转一周，则所得几何体的表面积是多少？
已知：如图，四边形ABCD及一点P．