题目内容
【题目】如图,四边形![]() 是矩形,点
是矩形,点![]() 是对角线
是对角线![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合),连接
重合),连接![]() ,过点
,过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() .设
.设![]() 的长为
的长为![]() .
.
(1)![]() ;当
;当![]() 时,
时,![]() ;
;
(2)①试探究:![]() 否是定值?若是,请求出这个值;若不是,请说明理由;
否是定值?若是,请求出这个值;若不是,请说明理由;
②连接![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值.
的最小值.
(3)当![]() 是等腰三角形时.请求出
是等腰三角形时.请求出![]() 的值;
的值;

【答案】(1)4,![]() ;(2)①为定值,值为
;(2)①为定值,值为![]() ;②
;②![]() ;(3)
;(3)![]() 或4
或4
【解析】
(1)作PM⊥AB于M交CD于N.根据三角函数和勾股定理求出AB,求出PN和BM的长,由△BMP∽△PNE,推出 ![]() 即可得出结果;
即可得出结果;
(2)① ![]() 为定值.证明方法类似(1); ②利用勾股定理求出
为定值.证明方法类似(1); ②利用勾股定理求出![]() ,根据三角形的面积公式得出二次函数,再利用二次函数的性质即可解决问题.
,根据三角形的面积公式得出二次函数,再利用二次函数的性质即可解决问题.
(3)分两种情形讨论求解,当点E在线段CD上时,当点E在DC的延长线上时,即可解决问题;
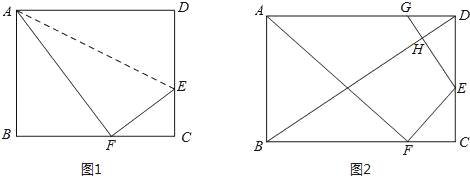
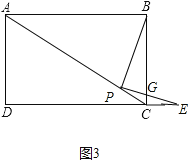
解:(1)作PM⊥AB于M交CD于N.如图1所示:
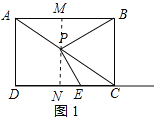
∵四边形ABCD是矩形, ∴BC=AD=3,∠ABC=90°,
∴sin∠BAC=![]()
∴AC=5, ∴AB=![]()
在Rt△APM中,PA=1,PM=![]() ,AM=
,AM=![]() ,
,
∴![]()
![]() ,
,
∵MN=AD=3,
∴PN=MN-PM=![]() ,
,
∵∠PMB=∠PNE=∠BPE=90°,
∴∠BPM+∠EPN=90°,∠EPN+∠PEN=90°,
∴∠BPM=∠PEN,
∴△BMP∽△PNE,
∴ 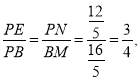
故答案为4,![]() ;
;
(2)①结论: ![]() 的值为定值
的值为定值![]() .
.
理由如下: 当点E在点C左侧时,如图1所示: 由PA=x,可得PM=![]()
∴AM![]()
∵△BMP∽△PNE,
∴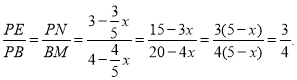
当点E在点C右侧时,如图2所示:
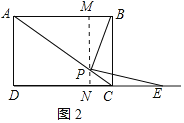
同理得出 ![]() . 综上所述:
. 综上所述:![]() 的值为定值
的值为定值![]() .
.
②在Rt△PBM中,![]()
∵ ![]() . ∴
. ∴![]() ,
,
∴![]()
∵0<x<5, ∴![]() 时,S有最小值=
时,S有最小值=![]() .
.
(3)①当点E在线段CD上时,连接BE交AC于F.
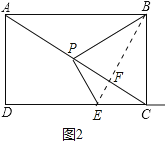
∵∠PEC>90°,所以只能EP=EC,
∴∠EPC=∠ECP,
∵∠BPE=∠BCE=90°,
∴∠BPC=∠BCP,
∴BP=BC,
∴BE垂直平分线段PC,
在Rt△BCF中,cos∠BCF![]() ,
,
∴![]() ∴
∴![]()
∴![]()
∴![]()
②当点E在DC的延长线上时,设BC交PE于G.
∵∠PCE>90°,所以只能CP=CE.
∴∠CPE=∠E,
∵∠GPB=∠GCE=90°,∠PGB=∠CGE,
∴∠PBG=∠E=∠CPE,
∵∠ABP+∠PBC=90°,
∠APB+∠CPE=90°,
∴AB=AP=4,
综上所述,x的值为![]() 或4.
或4.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案【题目】某校组织了2000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
成绩 | 频数 | 频率 |
| 20 |
|
| 16 | 0.08 |
|
| 0.15 |
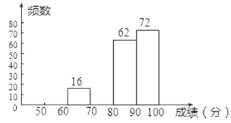
请你根据以上的信息,回答下列问题:
(1)![]() ,
,![]() ;
;
(2)在扇形统计图中,“成绩![]() 满足
满足![]() ”对应扇形的圆心角的度数是 ;
”对应扇形的圆心角的度数是 ;
(3)若将得分转化为等级,规定:![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() .这次全校参加竞赛的学生约有 人参赛成绩被评为“
.这次全校参加竞赛的学生约有 人参赛成绩被评为“![]() ”.
”.