ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΘ®‘ΡΕΝάμΫβΘ©»τ ΐ÷α…œΝΫΒψ![]() Θ§
Θ§![]() Υυ±μ ΨΒΡ ΐΖ÷±πΈΣ
Υυ±μ ΨΒΡ ΐΖ÷±πΈΣ![]() ΚΆ
ΚΆ![]() Θ§‘ρ”–ΘΚ
Θ§‘ρ”–ΘΚ
ΔΌ![]() Θ§
Θ§![]() ΝΫΒψΒΡ÷–Βψ±μ ΨΒΡ ΐΈΣ
ΝΫΒψΒΡ÷–Βψ±μ ΨΒΡ ΐΈΣ![]() ΘΜ
ΘΜ
ΔΎ![]() Θ§
Θ§![]() ΝΫΒψ÷°ΦδΒΡΨύάκ
ΝΫΒψ÷°ΦδΒΡΨύάκ![]() ΘΜ»τ
ΘΜ»τ![]() Θ§‘ρΩ…ΦρΜ·ΈΣ
Θ§‘ρΩ…ΦρΜ·ΈΣ![]() Θ°
Θ°
Θ®ΫβΨωΈ ΧβΘ© ΐ÷α…œΝΫΒψ![]() Θ§
Θ§![]() Υυ±μ ΨΒΡ ΐΖ÷±πΈΣ
Υυ±μ ΨΒΡ ΐΖ÷±πΈΣ![]() ΚΆ
ΚΆ![]() Θ§«“¬ζΉψ
Θ§«“¬ζΉψ![]() Θ°
Θ°
Θ®1Θ©«σ≥ω![]() Θ§
Θ§![]() ΝΫΒψΒΡ÷–Βψ
ΝΫΒψΒΡ÷–Βψ![]() ±μ ΨΒΡ ΐΘΜ
±μ ΨΒΡ ΐΘΜ
Θ®2Θ©Βψ![]() ¥”‘≠Βψ
¥”‘≠Βψ![]() Βψ≥ωΖΔœρ”“‘ΥΕ·Θ§Ψ≠Ιΐ
Βψ≥ωΖΔœρ”“‘ΥΕ·Θ§Ψ≠Ιΐ![]() ΟκΚσΒψ
ΟκΚσΒψ![]() ΒΫ
ΒΫ![]() ΒψΒΡΨύάκ «Βψ
ΒψΒΡΨύάκ «Βψ![]() ΒΫ
ΒΫ![]() ΒψΨύάκΒΡ
ΒψΨύάκΒΡ![]() ±ΕΘ§«σΒψ
±ΕΘ§«σΒψ![]() ΒΡ‘ΥΕ·ΥΌΕ» «ΟΩΟκΕύ…ΌΗωΒΞΈΜ≥ΛΕ»ΘΩ
ΒΡ‘ΥΕ·ΥΌΕ» «ΟΩΟκΕύ…ΌΗωΒΞΈΜ≥ΛΕ»ΘΩ
Θ® ΐ―ßΥΦΩΦΘ©
Θ®3Θ©Βψ![]() “‘ΟΩΟκ
“‘ΟΩΟκ![]() ΗωΒΞΈΜΒΡΥΌΕ»¥”‘≠Βψ
ΗωΒΞΈΜΒΡΥΌΕ»¥”‘≠Βψ![]() ≥ωΖΔœρ”“‘ΥΕ·Θ§Ά§ ±Θ§Βψ
≥ωΖΔœρ”“‘ΥΕ·Θ§Ά§ ±Θ§Βψ![]() ¥”Βψ
¥”Βψ![]() ≥ωΖΔ“‘ΟΩΟκ
≥ωΖΔ“‘ΟΩΟκ![]() ΗωΒΞΈΜΒΡΥΌΕ»œρΉσ‘ΥΕ·Θ§Βψ
ΗωΒΞΈΜΒΡΥΌΕ»œρΉσ‘ΥΕ·Θ§Βψ![]() ¥”Βψ
¥”Βψ![]() ≥ωΖΔΘ§“‘ΟΩΟκ
≥ωΖΔΘ§“‘ΟΩΟκ![]() ΗωΒΞΈΜΒΡΥΌΕ»œρ”“‘ΥΕ·Θ§
ΗωΒΞΈΜΒΡΥΌΕ»œρ”“‘ΥΕ·Θ§![]() ΓΔ
ΓΔ![]() Ζ÷±πΈΣ
Ζ÷±πΈΣ![]() ΓΔ
ΓΔ![]() ΒΡ÷–ΒψΘ°ΥΦΩΦΘΚ‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§
ΒΡ÷–ΒψΘ°ΥΦΩΦΘΚ‘Ύ‘ΥΕ·Ιΐ≥Χ÷–Θ§![]() ΒΡ÷Β «ΖώΖΔ…ζ±δΜ·ΘΩ»γΙϊΟΜ”–±δΜ·Θ§«κ«σ≥ω’βΗω÷ΒΘΜ»γΙϊΖΔ…ζ±δΜ·Θ§«κΥΒΟςάμ”…Θ°
ΒΡ÷Β «ΖώΖΔ…ζ±δΜ·ΘΩ»γΙϊΟΜ”–±δΜ·Θ§«κ«σ≥ω’βΗω÷ΒΘΜ»γΙϊΖΔ…ζ±δΜ·Θ§«κΥΒΟςάμ”…Θ°
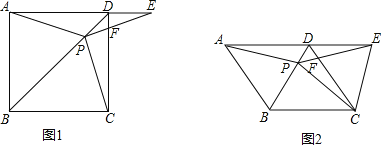
ΓΨ¥πΑΗΓΩΘ®1Θ©3ΘΜΘ®2Θ©ΒψDΒΡ‘ΥΕ·ΥΌΕ» «ΟΩΟκ![]() ΗωΒΞΈΜ≥ΛΕ»Θ§ΜρΟΩΟκ4ΗωΒΞΈΜ≥ΛΕ»ΘΜΘ®3Θ©≤Μ±δΘ§
ΗωΒΞΈΜ≥ΛΕ»Θ§ΜρΟΩΟκ4ΗωΒΞΈΜ≥ΛΕ»ΘΜΘ®3Θ©≤Μ±δΘ§![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΖ«ΗΚ ΐΒΡ–‘÷ ΚΆ÷–ΒψΉχ±ξΒΡ«σΖ®Φ¥Ω…ΒΟΒΫΫα¬έΘΜ
Θ®2Θ©…ηΒψDΒΡ‘ΥΕ·ΥΌΕ»ΈΣvΘ§ΔΌΒ±ΒψD‘ΥΕ·ΒΫΒψCΉσ±Ώ ±Θ§ΔΎΒ±ΒψD‘ΥΕ·ΒΫΒψC”“±Ώ ±Θ§ΗυΨίΧβ“βΝ–ΖΫ≥ΧΦ¥Ω…ΒΟΒΫΫα¬έΘΜ
Θ®3Θ©…η‘ΥΕ· ±ΦδΈΣtΘ§‘ρΒψEΕ‘”ΠΒΡ ΐ «tΘ§ΒψMΕ‘”ΠΒΡ ΐ «27tΘ§ΒψNΕ‘”ΠΒΡ ΐ «8ΘΪ10tΘ°ΗυΨίΧβ“β«σΒΟPΒψΕ‘”ΠΒΡ ΐ «![]() ΘΫ13tΘ§QΒψΕ‘”ΠΒΡ ΐ «
ΘΫ13tΘ§QΒψΕ‘”ΠΒΡ ΐ «![]() ΘΫ4ΘΪ5tΘ§”Ύ ««σΒΟΫα¬έΘ°
ΘΫ4ΘΪ5tΘ§”Ύ ««σΒΟΫα¬έΘ°
ΫβΘΚΘ®1Θ©ΓΏ|a+2|+Θ®b-8Θ©2020=0
Γύa=-2Θ§b=8Θ§
ΓύAΓΔBΝΫΒψΒΡ÷–ΒψC±μ ΨΒΡ ΐ «ΘΚ![]() ΘΫ3ΘΜ
ΘΫ3ΘΜ
Θ®2Θ©…ηΒψDΒΡ‘ΥΕ·ΥΌΕ»ΈΣvΘ§
ΔΌΒ±ΒψD‘ΥΕ·ΒΫΒψCΉσ±Ώ ±ΘΚ”…Χβ“βΘ§”–2v-Θ®-2Θ©=2Θ®3-2vΘ©Θ§
Ϋβ÷°ΒΟvΘΫ![]()
ΔΎΒ±ΒψD‘ΥΕ·ΒΫΒψC”“±Ώ ±ΘΚ”…Χβ“βΘ§”–2v-Θ®-2Θ©=2Θ®2v-3Θ©Θ§
Ϋβ÷°ΒΟv=4ΘΜ
ΓύΒψDΒΡ‘ΥΕ·ΥΌΕ» «ΟΩΟκ![]() ΗωΒΞΈΜ≥ΛΕ»Θ§ΜρΟΩΟκ4ΗωΒΞΈΜ≥ΛΕ»ΘΜ
ΗωΒΞΈΜ≥ΛΕ»Θ§ΜρΟΩΟκ4ΗωΒΞΈΜ≥ΛΕ»ΘΜ
Θ®3Θ©…η‘ΥΕ· ±ΦδΈΣtΘ§‘ρΒψEΕ‘”ΠΒΡ ΐ «tΘ§ΒψMΕ‘”ΠΒΡ ΐ «-2-7tΘ§ΒψNΕ‘”ΠΒΡ ΐ «8+10tΘ°
ΓΏP «MEΒΡ÷–ΒψΘ§
ΓύPΒψΕ‘”ΠΒΡ ΐ «![]() ΘΫ13tΘ§
ΘΫ13tΘ§
”÷ΓΏQ «ONΒΡ÷–ΒψΘ§
ΓύQΒψΕ‘”ΠΒΡ ΐ «![]() ΘΫ4+5tΘ§
ΘΫ4+5tΘ§
ΓύMN=Θ®8+10tΘ©-Θ®-2-7tΘ©=10+17tΘ§OE=t
PQ=Ȯ4+5tȩ-Ȯ-1-3tȩ=5+8tȧ
Γύ![]()
Γύ![]() ΒΡ÷Β≤Μ±δΘ§Β»”Ύ2Θ°
ΒΡ÷Β≤Μ±δΘ§Β»”Ύ2Θ°

 ΒψΨΠ–¬ΫΧ≤Ρ»ΪΡήΫβΕΝœΒΝ–¥πΑΗ
ΒψΨΠ–¬ΫΧ≤Ρ»ΪΡήΫβΕΝœΒΝ–¥πΑΗ –Γ―ßΫΧ≤ΡΆξ»ΪΫβΕΝœΒΝ–¥πΑΗ
–Γ―ßΫΧ≤ΡΆξ»ΪΫβΕΝœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΩΈΧβ–ΓΉι¥”Ρ≥ –2000ΟϊΨ≈ΡξΦΕΡ–…ζ÷–Θ§ΥφΜζ≥ι»ΓΝΥ1000ΟϊΫχ––50ΟΉ≈ή≤β ‘Θ§≤ΔΗυΨί≤β ‘ΫαΙϊ÷Τ≥…ΝΥ»γœ¬ΒΡΆ≥ΦΤ±μΘ°
Β»ΦΕ | »Υ ΐ | ΑΌΖ÷±» |
”≈–ψ | 200 | 20% |
ΝΦΚΟ | 600 | 60% |
ΦΑΗώ | 150 | 15% |
≤ΜΦΑΗώ | 50 |
|
Θ®1Θ©![]() ΒΡ÷ΒΈΣ______ΘΜ
ΒΡ÷ΒΈΣ______ΘΜ
Θ®2Θ©«κ¥”±μΗώ÷–»Έ“β―ûÓΜΝ– ΐΨίΘ§Μφ÷ΤΚœάμΒΡΆ≥ΦΤΆΦά¥±μ ΨΘΜΘ®Μφ÷Τ“Μ÷÷Φ¥Ω…Θ©
Θ®3Θ©ΙάΦΤ’β20000ΟϊΨ≈ΡξΦΕΡ–…ζ÷–50ΟΉ≈ή¥οΒΫΝΦΚΟΚΆ”≈–ψΒ»ΦΕΒΡΉή»Υ ΐΘ°