��Ŀ����
����Ŀ���ڵȱ�![]() �У���
�У���![]() Ϊ
Ϊ![]() ��һ�㣬����
��һ�㣬����![]() ��ֱ��
��ֱ��![]() ��
��![]() �ֱ��ཻ�ڵ�
�ֱ��ཻ�ڵ�![]() ����
����![]() ��
��
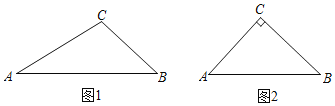
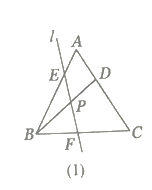
��1����ͼ��1����д��ͼ��������![]() ���Ƶ������Σ���ѡ�����е�һ�Ը���֤����
���Ƶ������Σ���ѡ�����е�һ�Ը���֤����
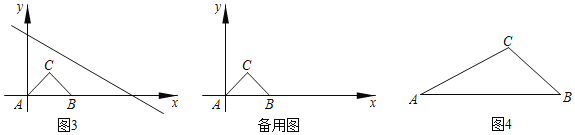
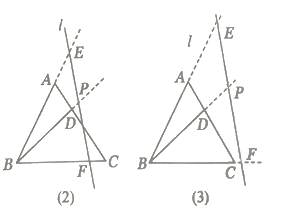
��2����ֱ��![]() ����ƽ�Ƶ�ͼ��2����ͼ��3����λ��ʱ�������������䣬��1���еĽ����Ƿ���Ȼ����?��������д����(��֤��)��������������˵�����ɣ�
����ƽ�Ƶ�ͼ��2����ͼ��3����λ��ʱ�������������䣬��1���еĽ����Ƿ���Ȼ����?��������д����(��֤��)��������������˵�����ɣ�
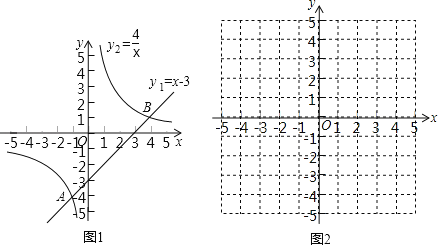
��3��̽��:��ͼ��1������![]() ����ʲô����ʱ(������������)��
����ʲô����ʱ(������������)��![]() ?��д��̽���������˵������(˵��:�����в��ú���δ��ʶ����ĸ)��
?��д��̽���������˵������(˵��:�����в��ú���δ��ʶ����ĸ)��
���𰸡���1�� ��BPF�ס�EBF����BPF�ס�BCD����2�����������ֱ�Ϊ��BPF�ס�EBF����BPF�ס�BCD����3����BDƽ�֡�ABCʱ��PF=![]() PE��
PE��
��������
��1�������Ƕ�Ӧ��ȵ��������������������ҳ���BPF�ס�EBF����BPF�ס�BCD�������������ζ�����һ�������Ǻ�һ��60������֤����
��2��������֤��ͬ��1����
��3���ȿ�PF=![]() PE�ܵó�ʲô���ۣ����ݡ�BPF�ס�EBF���ɵ�BF2=PFPE=3PF2�����
PE�ܵó�ʲô���ۣ����ݡ�BPF�ס�EBF���ɵ�BF2=PFPE=3PF2�����![]() ����Ϊ
����Ϊ![]() ���ɵá�PFB=90�������PBF=30�����ɴ˿ɵõ�BDƽ�֡�ABCʱ��PF=
���ɵá�PFB=90�������PBF=30�����ɴ˿ɵõ�BDƽ�֡�ABCʱ��PF=![]() PE��
PE��
�⣺��1����BPF�ס�EBF����BPF�ס�BCD��֤�����£�
�ߡ�ABC�ǵȱ������Σ�
���ABC=��ACB=��BAC=60����
�ߡ�BPF=60��
���BPF=��EBF=60����
�ߡ�BFP=��BFE��
���BPF�ס�EBF��
�ߡ�BPF=��BCD=60������PBF=��CBD��
���BPF�ס�BCD��
��2�����������ֱ�Ϊ��BPF�ס�EBF����BPF�ס�BCD��֤�����£�
��ͼ��2���ߡ�BPF=��EBF=60������BFP=��BFE��
���BPF�ס�EBF��
�ߡ�BPF=��BCD=60������PBF=��CBD��
���BPF�ס�BCD��
��ͼ��3����ͬ����֤��BPF�ס�EBF����BPF�ס�BCD��
��3����BDƽ�֡�ABCʱ��PF=![]() PE��
PE��
���ɣ���BDƽ�֡�ABC�����ABP=��PBF=30����
�ߡ�BPF=60�������BFP=90����
��PF=![]() PB
PB
�֡ߡ�BEF=60��30��=30��=��ABP��
��PB=PE��
��PF=![]() PE��
PE��

 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�����Ŀ���̳�����ij�ֱ��䣬���ֱ���ÿ̨����Ϊ2500Ԫ����֪ԭ���ۼ�Ϊÿ̨2900Ԫʱ��ƽ��ÿ�����۳�8̨������ԭ���ۼ۵Ļ�����ÿ̨����50Ԫ����ƽ��ÿ��ɶ��۳�4̨����ÿ̨�����ʵ���ۼ۱�ԭ���ۼ۽�����![]() Ԫ��
Ԫ��
��1�������
ÿ���������/̨ | ÿ̨��������/Ԫ | |
����ǰ | 8 | 400 |
���ۺ� |
��2���̳�Ϊʹ���ֱ���ƽ��ÿ�����������ﵽ���ʱ����ÿ̨�����ʵ���ۼ�Ӧ��Ϊ����Ԫ��