题目内容
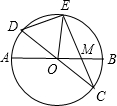
如图,在半径为4的⊙O中,AB,CD是两条直径,M是OB的中点,CM的延长线交⊙O于点E,设DE=| a |
(1)用含x和a的代数式表示MC的长,并求证:x2-
| 64-a |
(2)当a=15,且EM>MC时,求sin∠EOM的值;
(3)根据图形写出EM的长的取值范围.试问:在弧DB上是否存在一点E,使EM的长是关于x的方
 程x2-
程x2-| 64-a |
分析:(1)根据直径所对的圆周角是直角得到直角三角形CDE,再根据勾股定理求得CE的长,进一步求得MC的长.根据相交弦定理进行证明.
(2)根据(1)中的方程即可求得x的值,即可以求得EM,CM的长.此时会发现三角形EOM是等腰三角形,作其底边上的高,根据等腰三角形的三线合一和勾股定理求得其底边上的高,再进一步求得sin∠EOM的值;
(3)根据图形可知EM一定大于BM的长,即2,而小于AM的长,即6.首先根据方程有两个相等的实数根,利用△=0求得a的值,再进一步求得EM的长.根据EM,OE,OM的长,不难发现这是一个直角三角形,即可求得sin∠EOM的值.
(2)根据(1)中的方程即可求得x的值,即可以求得EM,CM的长.此时会发现三角形EOM是等腰三角形,作其底边上的高,根据等腰三角形的三线合一和勾股定理求得其底边上的高,再进一步求得sin∠EOM的值;
(3)根据图形可知EM一定大于BM的长,即2,而小于AM的长,即6.首先根据方程有两个相等的实数根,利用△=0求得a的值,再进一步求得EM的长.根据EM,OE,OM的长,不难发现这是一个直角三角形,即可求得sin∠EOM的值.
解答:解:(1)∵CD是直径
∴∠CED=90度
在直角三角形CDE中,DE=
,CD=8
根据勾股定理,得CE=
∴MC=
-x
根据相交弦定理,得
AM•BM=CM•EM
即x(
-x)=6×2
得x2-
•x+12=0.
(2)当a=15时,根据(1)中的方程,有
x2-7x+12=0
解得x=3或x=4
又EM>MC,则
EM=4,MC=3
因为EM=EO=4,作EF⊥OB于F,则OF=1
根据勾股定理,得EF=
所以sin∠EOM=
.
(3)根据图形,显然2<x<6.
根据EM的长是关于x的方程x2-
•x+12=0的相等实数根,则
△=64-a-48=0
∴a=16
把a=16代入方程,解得x=2
即EM=2
又∵OE=4,OM=2
∴sin∠EOM=
.
∴∠CED=90度
在直角三角形CDE中,DE=
| a |
根据勾股定理,得CE=
| 64-a |
∴MC=
| 64-a |
根据相交弦定理,得
AM•BM=CM•EM
即x(
| 64-a |
得x2-
| 64-a |
(2)当a=15时,根据(1)中的方程,有
x2-7x+12=0
解得x=3或x=4
又EM>MC,则
EM=4,MC=3
因为EM=EO=4,作EF⊥OB于F,则OF=1
根据勾股定理,得EF=
| 15 |
所以sin∠EOM=
| ||
| 4 |
(3)根据图形,显然2<x<6.
根据EM的长是关于x的方程x2-
| 64-a |
△=64-a-48=0
∴a=16
把a=16代入方程,解得x=2
| 3 |
即EM=2
| 3 |
又∵OE=4,OM=2
∴sin∠EOM=
| ||
| 2 |
点评:综合运用了数形结合的知识.既要熟悉一元二次方程根的判别式,还要熟悉相交弦定理、勾股定理及其逆定理和锐角三角函数的定义.在计算的过程中能够根据线段的长发现特殊的三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
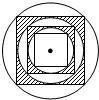 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
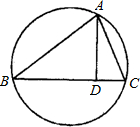 如图,在半径为R的圆中作一内接△ABC,使BC边上的高AD=h(定值),这样的三角形可作出无数个,但AB•AC为定值,其值为
如图,在半径为R的圆中作一内接△ABC,使BC边上的高AD=h(定值),这样的三角形可作出无数个,但AB•AC为定值,其值为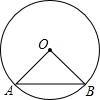 如图,在半径为2的⊙O中,弦AB的长为2
如图,在半径为2的⊙O中,弦AB的长为2 (2012•陕西)如图,在半径为5的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
(2012•陕西)如图,在半径为5的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( ) (2013•上海模拟)如图,在半径为1的扇形AOB中,∠AOB=90°,点P是
(2013•上海模拟)如图,在半径为1的扇形AOB中,∠AOB=90°,点P是