题目内容
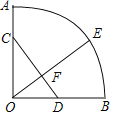
【题目】如图线段OA=12,线段OA绕点O旋转90°,形成扇形OAB,点D为OB的中点,点E为弧AB上的动点,连接OE,与CD的交点为F,点C在OA上,AC=4.
(1)①CD= ;②当BE弧长为4π时,∠BOE= .
(2)当四边形ODEC面积最大时,求EF.
(3)在点E的运动过程中,是否存在一个时刻使CE+2DE有最小值?若存在请直接写出答案;若不存在,请说明理由.
【答案】(1)①10;②60°;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)运用勾股定理计算CD,由弧长公式可求出∠BOE;
(2)四边形面积最大时,两三角形的高的和等于半径,即可求得EF;
(3)延长OB至点G,使BG=OB,连接GE、GC、DE.证明△DOE~△EOG,得到EG=2DE,所以CE+2DE=CE+EG,当C、E、G三点在同一直线上上时,CE+EG最小,此时CE+EG=CG=![]() =
=![]() =8
=8![]() ,即CE+2DE有最小值为8
,即CE+2DE有最小值为8![]() .
.
解:(1)①在Rt△OCD中,∠COD=90°,OC=OA﹣AC=12﹣4=8,OD=![]() OB=
OB=![]() =6,
=6,
∴![]() =
=![]() =10,
=10,
故答案为:10;
②设∠BOE=n°,由弧长公式得:![]() ,解得:n=6
,解得:n=6
∴∠BOE=60°;
故答案为:60°;
(2)分别过O、E作OM⊥CD于M,EN⊥CD于N,
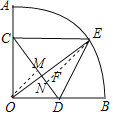
∵CD=10,
∴S四边形ODEC=S△OCD+S△CDE=![]() CD(OM+EN)≤
CD(OM+EN)≤![]() CDOE=
CDOE=![]() ×10×12=60;
×10×12=60;
此时,OM、EN、OE重合,
∵OMCD=OCOD
∴10×OM=6×8,OM=![]() ,
,
∴![]() =
=![]() ;
;
(3)延长OB至点G,使BG=OB,连接GE、GC、DE.

∴![]()
∵点D为OB的中点,OB=OE,
∴![]() ,
,
∴![]() ,
,
又∠DOE=∠EOG,
∴△DOE~△EOG,
![]() ,
,
即EG=2DE,
∴CE+2DE=CE+EG,
当C、E、G三点在同一直线上上时,CE+EG最小,
CO=OA﹣AC=12﹣4=8,OG=OB+BG=12+12=24,
此时CE+EG=CG=![]() =
=![]() =8
=8![]() ,
,
故CE+2DE有最小值为8![]() .
.

【题目】在精准扶贫中,李师傅在扶贫工作者的指导下,计划用8个大棚种植香瓜和甜瓜根据种植经验及市场情况,他打算两个品种同时种,一个大只种一个品种的瓜并预测明年两种瓜的产量、销售价格及成本如下:
品种项目 | 产量(斤/每棚) | 销售价(元/每斤) | 成本(元/棚) |
香瓜 | 2000 | 12 | 8000 |
甜瓜 | 4500 | 3 | 5000 |
根据以上信息,求李师傅至少种植多少个大棚的香瓜,才能使他获得的利润不低于10万元.