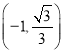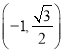Question

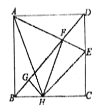
【题目】如图，直线 分别交x轴、y轴于A、B两点，已知点C坐标为（6,0），若直线AB上存在点P，使∠OPC=90°，则m的取值范围是。

Answer 1

【答案】
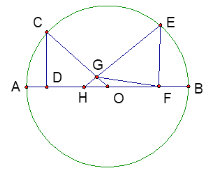
【解析】解 ：如图 ：

要使∠OPC=90，则直线AB必经过以OC为直径的圆，
如图直线AB切圆于P,
∴∠MPA=90°
∵点C(6,0)，
∴OC=6，
∴OM=PM=3，
∵直线y=x+m，
∴ A（,0）; B(0,m);
∴OA=,OB=m;
∴OB∶OA=2∶3，
∵∠OAB=∠PAM,∠AOB=∠APM=90，
∴△AOB∽△APM，
∴PM∶PA=OB∶OA=2∶3，
∴PA=，
∴MA=
∴OA=3+或3-
∵点A的横坐标为m；
∴=3+或 =3-
∴m=2+或m=2-
∴m的取值范围是2+≤m≤2-
故答案为 :2+≤m≤ 2-.
要使∠OPC=90，则直线AB必经过以OC为直径的圆，如图直线AB切圆于P,根据切线的性质得出∠MPA=90°，由C点的坐标得出OC=6，进而得出OM=PM=3，根据直线与坐标轴的交点的特点得出A,B两点的坐标，进而得出OA,OB的长度，从而得出OB,与OA的比值，再判断出△AOB∽△APM，由相似三角形对应边成比例得出PM∶PA=OB∶OA=2∶3，进而求出PA,MA,OA的长度，根据点A的横坐标，得出关于m的方程，求解得出m的值，进而就求出m的取值范围。