题目内容
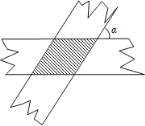
【题目】如图,两条宽度都为![]() 的纸条,交叉重叠放在一起,,它们的交角
的纸条,交叉重叠放在一起,,它们的交角![]() 为
为![]() ,则它们重叠部分(阴影部分)的面积为( )
,则它们重叠部分(阴影部分)的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
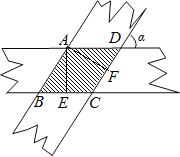
过点A作AE⊥BC,AF⊥CD,垂足分别为E,F,证明△ABE≌△ADF,从而证明四边形ABCD是菱形,再利用勾股定理求出BC的长,最后根据菱形的面积公式算出重叠部分的面积即可.
过点A作AE⊥BC,AF⊥CD,垂足分别为E,F,如图所示,
∴∠AEB=∠AFD=90°,
∵AD∥CB,AB∥CD,
∴四边形ABCD是平行四边形,
∵纸条宽度都为3cm,
∴AE=AF=3cm,
在△ABE和△ADF中,
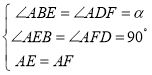 ,
,
∴△ABE≌△ADF(AAS),
∴AB=AD,∠BAE=30°,
∴四边形ABCD是菱形,
∴BC=AB,
设![]() ,则
,则![]() ,
,
在Rt△ABE中,![]() ,
,
解得,![]() (负值舍去),
(负值舍去),
∴BC=AB=![]() cm,
cm,
∴重叠部分(图中阴影部分)的面积=3×![]() =
=![]() (cm2),
(cm2),
故选D.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目