题目内容
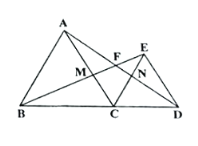
【题目】如图,己知点C是线段BD上一点,以BC、 DC为一边在BD的同一侧作等边△ABC和等边△ECD,连接AD, BE相交于点F, AC和BE交于点M, AD, CE交于点N,(注:等边三角形的每一个内角都等于60° )
(1) 求证: AD=BE
(2) 线段CM与CN相等吗?请证明你的结论。
(3) 求∠BFD的度数。
【答案】(1)见解析;(2)BM=AN 理由见解析;(3)120°.
【解析】
(1)根据已知条件易证△ACD≌△BCE,即可证明AD=BE;
(2)易证△BCM≌△ACN,即可进行判断;
(3)根据△ACD≌△BCE,∠EBC+∠ADC=∠EBC+∠BEC=∠ECD=60°,故根据△BDF的内角和即可求解.
(1)证明:∵△ABC、△DCE均是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠ACD=∠DCE+∠ACD,即∠BCE=∠ACD,
∴△ACD≌△BCE(SAS),
∴BD=AE;
(2)∵△ACD≌△BCE
∴∠CBM=∠CAN
∵∠BCM=∠ECD=60°,∴∠ACN=60°,
又BC=AC
∴△BCM≌△ACN (ASA)
∴BM=AN.
(3)∵△ACD≌△BCE,
∴∠EBC+∠ADC=∠EBC+∠BEC=∠ECD=60°,
∴在△BDF中∠BFD=180°-(∠EBC+∠ADC)=120°.

练习册系列答案
相关题目