题目内容
【题目】四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.
(1)利用图1,求证:四边形ABCD是菱形. 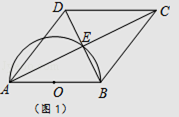
(2)如图2,若CD的延长线与半圆相切于点F,已知直径AB=8. ①连结OE,求△OBE的面积.
②求扇形AOE的面积.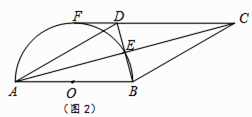
【答案】
(1)证明:∵AE=EC,BE=ED,
∴四边形ABCD是平行四边形,
∵AB为直径,且过点E,
∴∠AEB=90°,即AC⊥BD,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形;
(2)解:①连结OF,
∵DC的延长线于半圆相切于点F,
∴OF⊥CF,
∵FC∥AB,
∴OF即为△ABD中AB边上的高,
∴S△ABD= ![]() AB×OF=
AB×OF= ![]() ×8×4=16,
×8×4=16,
∵点O是AB中点,点E是BD的中点,
∴S△OBE= ![]() S△ABD=4;
S△ABD=4;
②过点D作DH⊥AB于点H,
∵AB∥CD,OF⊥CF,
∴FO⊥AB,
∴∠F=∠FOB=∠DHO=90°,
∴四边形OHDF为矩形,即DH=OF=4,
∵在Rt△DAH中,sin∠DAB= ![]() =
= ![]() ,
,
∴∠DAH=30°,
∵D点O,E分别为AB,BD中点,
∴OE∥AD,
∴∠EOB=∠DAH=30°,
∴∠AOE=180°﹣∠EOB=150°,
∴S扇形AOE= ![]() =
= ![]() π.
π.

【解析】(1)首先利用对角线互相平分的四边形是平行四边形得出四边形ABCD是平行四边形,进而利用菱形的判定方法得出答案;(2)①首先求出△ABD的面积进而得出S△OBE= ![]() S△ABD;②首先求出扇形AOE的圆心角,进而利用扇形面积求出答案.
S△ABD;②首先求出扇形AOE的圆心角,进而利用扇形面积求出答案.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 240 | 180 |
(1)求a,b的值;
(2)治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.